题目内容
2.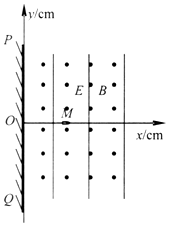 如图所示,在坐标系xOy平面的x>0区域内,存在电场强度大小E=2×105N/C、方向垂直于x轴的匀强电场和磁感应强度大小B=0.20T、方向与xOy平面垂直向外的匀强磁场.在y轴上有一足够长的荧光屏PQ,在x轴上的M(10,0)点处有一粒子发射枪向x轴正方向连续不断地发射大量质量m=6.4×10-27kg、电荷量q=3.2×10-19C的带正电粒子(重力不计),粒子恰能沿x轴做匀速直线运动.若撤去电场,并使粒子发射枪以M点为轴在xOy平面内以角速度ω=2πrad/s顺时针匀速转动(整个装置都处在真空中).
如图所示,在坐标系xOy平面的x>0区域内,存在电场强度大小E=2×105N/C、方向垂直于x轴的匀强电场和磁感应强度大小B=0.20T、方向与xOy平面垂直向外的匀强磁场.在y轴上有一足够长的荧光屏PQ,在x轴上的M(10,0)点处有一粒子发射枪向x轴正方向连续不断地发射大量质量m=6.4×10-27kg、电荷量q=3.2×10-19C的带正电粒子(重力不计),粒子恰能沿x轴做匀速直线运动.若撤去电场,并使粒子发射枪以M点为轴在xOy平面内以角速度ω=2πrad/s顺时针匀速转动(整个装置都处在真空中).(1)判断电场方向,求粒子离开发射枪时的速度;
(2)带电粒子在磁场中运动的轨迹半径;
(3)荧光屏上闪光点的范围;
(4)荧光屏上闪光点从最低点移动到最高点所用的时间.
分析 (1)粒子做匀速直线运动,所示合力为零,由平衡条件可以求出粒子的运动速度;
(2)粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律列方程可以求出粒子的轨道半径;
(3)根据题意作出粒子电子打在荧光屏上的范围图示,然后由数学知识求出荧光屏上闪光点的范围;
(4)根据几何关系求出放射源的偏转角,然后求出放射源转动的时间,再求出带电粒子在磁场中运动的时间差,求和即可.
解答 解:(1)由粒子在复合场中做匀速运动,根据左手定则可知,粒子受到的洛伦兹力的方向向下,所以电场力的方向以及电场的方向都向上,根据二力平衡有:qE=qvB;
所以:v=$\frac{E}{B}=\frac{2×1{0}^{5}}{0.2}=1{0}^{6}$m/s
(2)撤去电场后,洛伦兹力提供向心力,有:qvB=m$\frac{{v}^{2}}{R}$;
故粒子在磁场中运动的轨迹半径:
R=$\frac{mE}{q{B}^{2}}$=$\frac{6.4×10{\;}^{-27}×2×10{\;}^{5}}{3.2×10-19×0.2{\;}^{2}}$m=0.1m;
(3)粒子运动轨迹画出右图所示,可知,粒子恰好与光屏相切时,最上端打在B点;粒子到光屏的距离最大等于2R时,最下端打在A点:
则:dOA=$\sqrt{(2R)^{2}-O{M}^{2}}$=$\sqrt{0.{2}^{2}-0.{1}^{2}}$=0.173m
dOB=R=0.1m
dAB=0.173+0.1=0.273m;
(4)由几何关系可知,∠OMA=60°,可知当粒子速度的方向与x轴的夹角为30°时,射出的粒子到达A点;而沿-x方向射出的粒子能到达B点,该过程放射源转过的角度:
θ=180°-30°=150°
又:150°=$\frac{5π}{6}$
所以放射源转动的时间:${t}_{0}=\frac{θ}{ω}$=$\frac{\frac{5}{6}π}{2π}=\frac{5}{12}$s≈0.42s
粒子在磁场中运动的周期:T=$\frac{2πm}{qB}$=$\frac{2×3.14×6.4×1{0}^{-27}}{3.2×1{0}^{-19}×0.2}$=6.28×10-7s
可知粒子在磁场中运动的时间差可以忽略不计,所以荧光屏上闪光点从最低点移动到最高点所用的时间近似等于0.42s.
答:(1)电场的方向向上,粒子离开发射枪时的速度为106m/s;
(2)带电粒子在磁场中做圆周运动的轨道半径为0.1m;
(3)荧光屏上闪光点的范围为0.273m.
(4)荧光屏上闪光点从最低点移动到最高点所用的时间为0.42s.
点评 粒子做匀速圆周运动,由平衡条件可以求出粒子的运动速度,粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律列方程,可以求出粒子运动的轨道半径;第三问是本题的难点,根据题意作出粒子的运动轨迹是解题的关键.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 如图所示,在水平面内有两根间距为d的光滑长直导轨ab、cd,b、d之间连接一个阻值为R的定值电阻,一根电阻也为R的导体棒MN垂直放置在导轨上,整个装置处于磁感应强度为B的竖直方向匀强磁场中.现对导体棒MN施加一个向右的力F,使其以速度v向右匀速运动,设MN两端电压为U,R上消耗的功率为P,导轨电阻不计下列结论正确的是( )
如图所示,在水平面内有两根间距为d的光滑长直导轨ab、cd,b、d之间连接一个阻值为R的定值电阻,一根电阻也为R的导体棒MN垂直放置在导轨上,整个装置处于磁感应强度为B的竖直方向匀强磁场中.现对导体棒MN施加一个向右的力F,使其以速度v向右匀速运动,设MN两端电压为U,R上消耗的功率为P,导轨电阻不计下列结论正确的是( )| A. | U=$\frac{1}{2}$Bdv,电流从b经过定值电阻R流向d | |
| B. | U=$\frac{1}{2}$Bdv,电流从d经过定值电阻R流向b | |
| C. | P=Fv | |
| D. | P=$\frac{Fv}{2}$ |

| A. | 该列简谐横波向x轴正方向传播 | |
| B. | 在t=0.25s时,质点P的加速度方向与y轴正方向相同 | |
| C. | 从t=0.10s到t=0.25s,该波沿x轴负方向传播了6m | |
| D. | 从t=0.10s到t=0.25s,质点P通过的路程为30m |
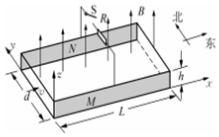 如图所示为利用海流发电的磁流体发电机原理示意图,矩形发电管道水平东西放置,整个管道置于方向竖直向上.磁感应强度大小为B的匀强磁场中,其上、下两面是绝缘板,南、北两侧面M、N是电阻可忽略的导体板,两导体板与开关S和定值电阻R相连,已知发电管道长为L,宽为d,高为h,海水在发电管道内以恒定速率v朝正东方向流动.发电管道内的海水在垂直流动方向的电阻为r,海水在管道内流动时受到摩擦阻力大小恒为f,不计地磁场的影响,则( )
如图所示为利用海流发电的磁流体发电机原理示意图,矩形发电管道水平东西放置,整个管道置于方向竖直向上.磁感应强度大小为B的匀强磁场中,其上、下两面是绝缘板,南、北两侧面M、N是电阻可忽略的导体板,两导体板与开关S和定值电阻R相连,已知发电管道长为L,宽为d,高为h,海水在发电管道内以恒定速率v朝正东方向流动.发电管道内的海水在垂直流动方向的电阻为r,海水在管道内流动时受到摩擦阻力大小恒为f,不计地磁场的影响,则( )| A. | 被侧面N的电势高 | |
| B. | 开关S断开时,M,N两端的电压为Bdv | |
| C. | 开关S闭合时,发电管道进、出口两端压力差F=f+$\frac{{B}^{2}{d}^{2}{v}^{2}}{R+r}$ | |
| D. | 开关S闭合时,电阻R上的功率为$\frac{{B}^{2}{d}^{2}{v}^{2}}{R}$ |
| A. | 物体重力势能减少$\frac{1}{4}$mgh | B. | 物体的机械能减少$\frac{1}{4}$mgh | ||
| C. | 物体的动能增加mgh | D. | 重力做功mgh |
 ,B车速度
,B车速度 ,因大雾能见度低,B车在距A车600m时才发现A车,此时B车立即刹车,但B车要减速1800m才能够停止,求:
,因大雾能见度低,B车在距A车600m时才发现A车,此时B车立即刹车,但B车要减速1800m才能够停止,求: 加速前进,问能否避免事故,若能够避免则两者最近时相距多远?
加速前进,问能否避免事故,若能够避免则两者最近时相距多远? 的初速度竖直上抛一个小球(不计空气阻力),当小球速度大小为10m/s时,以下判断正确的是(
的初速度竖直上抛一个小球(不计空气阻力),当小球速度大小为10m/s时,以下判断正确的是( )
)
 如图所示,长为L的轻质细线,一端固定在O点,另一端栓一质量为m的小球,让小球在空中某水平面内做匀速圆周运动,运动过程中O点与该水平面之间的距离为h,已知重力加速度为g,求:
如图所示,长为L的轻质细线,一端固定在O点,另一端栓一质量为m的小球,让小球在空中某水平面内做匀速圆周运动,运动过程中O点与该水平面之间的距离为h,已知重力加速度为g,求: