题目内容
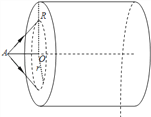
【题目】如图,圆柱形容器由粗细两部分组成,它们的横截面积之比为3:1,细的部分长L1=25cm,下端封闭,上端与粗的部分连通,内有h=15cm的水银柱封闭一定质量的气体A,水银上表面位于粗、细分界处。粗的部分上部有一可自由滑动的轻质活塞,活塞到分界面处的距离为L2=10cm,其内封闭有一定质量的气体B。现将活塞竖直向上缓慢提起,直到水银全部进入粗圆柱形容器内,已知初始时气体A的压强p0=75cmHg,整个过程温度不变,所有气体视为理想气体。求:

(1)求水银全部进入粗圆柱形容器中时气体A的压强;
(2)活塞移动的距离。
【答案】(1)30cmHg (2)19cm
【解析】
(1)A中气体发生等温变化,对A中封闭气体运用玻意耳定律,即可求出水银全部进入粗圆柱形容器中时气体A的压强;(2)B中气体发生等温变化,根据几何关系求出末态水银柱在B中的高度,对B中气体运用玻意耳定律结合几何关系,即可求出活塞移动的距离.
(1)A中气体发生等温变化.
初态:压强PA=P0,体积VA=(L1-h)S
末态:压强PA',体积VA'=L1S
对A中气体根据玻意耳定律可得:PAVA=PA'VA'
解得:PA'=30cmHg
(2)B中气体发生等温变化,
根据几何关系可得末状态粗圆柱形容器中水银的高度:![]()
初态:压强PB=P0-h=60cmHg,体积VB=L2S
末态:压强P'B=PA-h'=25cmHg,体积VB'=L'2S
根据玻意耳定律可得:PBVB=P'BVB'
解得:L'2=24cm
则![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目