题目内容
(1)试由万有引力定律推导:绕地球做圆周运动的人造卫星的周期T跟它轨道半径r的3/2次方成正比.(2)A、B两颗人造卫星的绕地球做圆周运动,它们的圆轨道在同一平面内,周期之比是
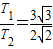 .若两颗卫星的最近距离等于地球半径R,求这两颗卫星的周期各是多少?从两颗卫星相距最近开始计时到两颗卫星相距最远至少经过多少时间?已知在地面附近绕地球做圆周运动的卫星周期为T.
.若两颗卫星的最近距离等于地球半径R,求这两颗卫星的周期各是多少?从两颗卫星相距最近开始计时到两颗卫星相距最远至少经过多少时间?已知在地面附近绕地球做圆周运动的卫星周期为T.
【答案】分析:(1)根据地球对人造卫星的万有引力提供向心力列式求解;
(2)根据第一问的结论求解出轨道半径之比,得到半径后进一步求解出A、B卫星的周期,最后根据相对运动求解从两颗卫星相距最近开始计时到两颗卫星相距最远的时间.
解答:解:(1)人造卫星绕地球做圆周运动,万有引力充当向心力:

解得:T=
地球质量M是常量,因此人造卫星绕地球运动的周期T与其轨道半径r的 次方成正比.
次方成正比.
(2)设B卫星轨道半径为r2,则A卫星轨道半径为r1=r2+R
 ①
①
解得r2=2R,r1=3R
可得:


T1=3
T2=2
设A、B两卫星从相距最近开始经过时间t第一次达相距最远,有
( )t=π ②
)t=π ②
解得时间t=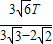 ≈3.1T
≈3.1T
答:(1)证明如上;
(2)这两颗卫星的周期分别是3 、2
、2 ;从两颗卫星相距最近开始计时到两颗卫星相距最远至少经过3.1T.
;从两颗卫星相距最近开始计时到两颗卫星相距最远至少经过3.1T.
点评:本题关键根据卫星的万有引力充当向心力列式求解出周期以半径的关系,然后运用该关系式分析第二问,不难.
(2)根据第一问的结论求解出轨道半径之比,得到半径后进一步求解出A、B卫星的周期,最后根据相对运动求解从两颗卫星相距最近开始计时到两颗卫星相距最远的时间.
解答:解:(1)人造卫星绕地球做圆周运动,万有引力充当向心力:

解得:T=

地球质量M是常量,因此人造卫星绕地球运动的周期T与其轨道半径r的
 次方成正比.
次方成正比.(2)设B卫星轨道半径为r2,则A卫星轨道半径为r1=r2+R
 ①
①解得r2=2R,r1=3R
可得:


T1=3

T2=2

设A、B两卫星从相距最近开始经过时间t第一次达相距最远,有
(
 )t=π ②
)t=π ②解得时间t=
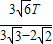 ≈3.1T
≈3.1T答:(1)证明如上;
(2)这两颗卫星的周期分别是3
 、2
、2 ;从两颗卫星相距最近开始计时到两颗卫星相距最远至少经过3.1T.
;从两颗卫星相距最近开始计时到两颗卫星相距最远至少经过3.1T.点评:本题关键根据卫星的万有引力充当向心力列式求解出周期以半径的关系,然后运用该关系式分析第二问,不难.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目