题目内容
【题目】如图所示,细绳OA与竖直方向成45°角,细绳OB水平;细绳OA、OB所能承受的最大拉力均为100![]() N,细绳OC能够承受足够大的拉力,重力加速度g取10 m/s2。求:
N,细绳OC能够承受足够大的拉力,重力加速度g取10 m/s2。求:
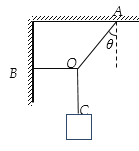
(1)当所悬挂重物的重力为50 N时,细线OA、OB的拉力分别是多大?
(2)为使细绳OA、OB均不被拉断,则细绳OC下端所悬挂重物的最大重力应为多大?
【答案】(1)TOA=50 ![]() N TOB=50 N (2)G=100 N
N TOB=50 N (2)G=100 N
【解析】
选结点O为研究对象,受力分析后应用平衡条件判断那根绳子先断,根据先断的绳子能承受的最大拉力求出最大重力。
(1) 选结点O为研究对象,受力分析并合成如图:
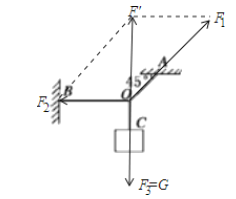
当重物为50N时,细线OA的拉力F1=![]()
OB的拉力F2=G=50N;
(2) 当OC下端所悬物重不断增大时,细线OA、OB所受的拉力同时增大
由于OA上的拉力F1大于OB上的拉力,所以在物重逐渐增大时,细线OA先被拉断
再假设OA线上的拉力刚好达到最大值F2max
处于将被拉断的临界状态,根据平衡条件有
F1sin45°=G;
得悬挂最大重力为
![]() 。
。

练习册系列答案
相关题目