Question

【题目】已知地球半径为R ， 引力常量为G ， 地球表面的重力加速度为g。不考虑地球自转的影响。
（1）推导第一宇宙速度v的表达式；
（2）若卫星绕地球做匀速圆周运动，运行轨道距离地面高度为h ， 飞行n圈，所用时间为t ， 求地球的平均密度。

Answer 1

【答案】
（1）

设卫星的质量为m，地球的质量为M，由于不考虑地球自转的影响，当卫星在地球表面时受到的万有引力近似等于重力，即

在地球表面附近的运行卫星，其轨道半径近似等于地球半径，万有引力提供向心力，根据万有引力定律和牛顿第二定律得：

以上两式联立解得：第一宇宙速度v的表达式为

（2）

设卫星圆轨道上运行周期为T，由题意得

卫星绕地球做匀速圆周运动，由万有引力定律和牛顿第二定律得

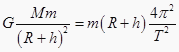，解得地球的质量为：

又地球体积 ，所以地球的平均密度

【解析】解:（1）设卫星的质量为m ， 地球的质量为M ， 由于不考虑地球自转的影响，当卫星在地球表面时受到的万有引力近似等于重力，即
在地球表面附近的运行卫星，其轨道半径近似等于地球半径，万有引力提供向心力，根据万有引力定律和牛顿第二定律得：
以上两式联立解得：第一宇宙速度v的表达式为 （2）设卫星圆轨道上运行周期为T，由题意得
卫星绕地球做匀速圆周运动，由万有引力定律和牛顿第二定律得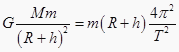
，解得地球的质量为：
又地球体积 ，所以地球的平均密度 。
【考点精析】解答此题的关键在于理解万有引力定律及其应用的相关知识，掌握应用万有引力定律分析天体的运动：把天体的运动看成是匀速圆周运动，其所需向心力由万有引力提供.即 F引=F向；应用时可根据实际情况选用适当的公式进行分析或计算.②天体质量M、密度ρ的估算．