题目内容
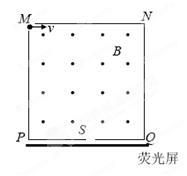
(18分)扭摆器是同步辐射装置中的插入件,能使粒子的运动轨迹发生扭摆,其简化模型如图所示:Ⅰ、Ⅱ两处宽度均为L的条形匀强磁场区边界竖直,Ⅰ区域磁场垂直纸面向外,Ⅱ区域磁场垂直纸面向里,磁感应强度大小均为B,两磁场区的间距可以调节。以Ⅰ区域左边界上的O点为坐标原点建立坐标系,y轴与左边界重合,x轴与磁场边界的交点分别为O1、O2和O3。一质量为m、电荷量为q的带正电的粒子,平行纸面从O点与y轴的夹角θ=30°射入Ⅰ区域,粒子重力不计。
(1)若粒子恰好从O1射出Ⅰ区域,粒子的速度应为多大?
(2)若粒子从Ⅰ区域右边界射出时速度与x轴的夹角为30°,调节两磁场区的间距,粒子恰好从O3射出Ⅱ区域,则粒子从O射入到从O3射出共经历了多长时间?
(1)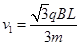 (2)
(2)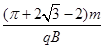
解析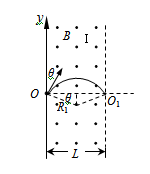
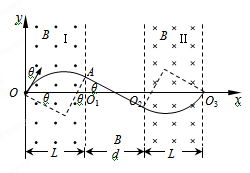
试题分析:(1)粒子从O1射出Ⅰ区域,轨迹如图
由几何关系
粒子在磁场中运动半径公式为: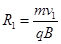
综合上式可得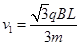
(2)粒子运动轨迹如图所示
设粒子运动速度为v2,半径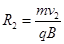
粒子在磁场中的运动周期为: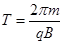
由几何关系可得,粒子在Ⅰ区域运动的圆心角为90°
即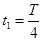
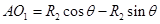
由于粒子在Ⅰ、Ⅱ区域运动半径相同,要使粒子从O3射出Ⅱ区域,则粒子在Ⅱ区域中运动时间与Ⅰ
区域相同,且粒子必须经过O1、O2的中点B,则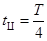
在Ⅰ、Ⅱ间隔区域运动时间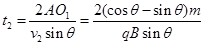
综上所述,粒子从相同O射入到O3射出共经历时间为: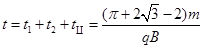
考点:本题考查带电粒子在匀强磁场中的运动。

练习册系列答案
相关题目
 )
)
 位置射出,求电子在磁场 Ⅰ 中运动的时间t.
位置射出,求电子在磁场 Ⅰ 中运动的时间t. OC,E点在D点正下方,位于x轴上,重力加速度为g。则:
OC,E点在D点正下方,位于x轴上,重力加速度为g。则:
 时刻粒子由C点进入第一象限,且恰好也能通过同一水平线上的D点,速度方向仍然水平。若粒子在第一象限中运动的周期与磁场变化周期相同,求交变磁场变化的周期;
时刻粒子由C点进入第一象限,且恰好也能通过同一水平线上的D点,速度方向仍然水平。若粒子在第一象限中运动的周期与磁场变化周期相同,求交变磁场变化的周期;
 小球距N点的距离s为多远。
小球距N点的距离s为多远。

 )。
)。
 大小、方向如何?
大小、方向如何?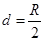 的电子在圆形磁场中运动了多长时间?
的电子在圆形磁场中运动了多长时间?