题目内容
（14分）如图所示，竖直平面坐标系xOy的第一象限，有垂直xOy面向外的水平匀强磁场和竖直向上的匀强电场，大小分别为B和E；第四象限有垂直xOy面向里的水平匀强电场，大小也为E；第三象限内有一绝缘光滑竖直放置的半径为R的半圆轨道，轨道最高点与坐标原点O相切，最低点与绝缘光滑水平面相切于N。一质量为m的带电小球从y轴上（y＞0）的P点沿x轴正方向进入第一象限后做圆周运动，恰好通过坐标原点O，且水平切入半圆轨道并沿轨道内侧运动，过N点水平进入第四象限，并在电场中运动（已知重力加速度为g）。
（1）判断小球的带电性质并求出其所带电荷量；
（2）P点距坐标原点O至少多高；
（3）若该小球以满足（2）中OP最小值的位置和对应速度进入第一象限，通过N点开始计时，经时间
小球距N点的距离s为多远。
（1）小球带正电，且
；（2）
（或
）；（3）2
R。
解析试题分析：（1）小球进入第一象限正交的电场和磁场后，在垂直磁场的平面内做圆周运动，说明重力与电场力平衡，qE＝mg① （1分）故电场力的方向是竖直向上的，由于电场强度的方向竖直向上，故小球带正电（1分）。且存在如下关系：② （1分）。
（2）小球在洛伦兹力作用下做匀速圆周运动，设匀速圆周运动的速度为v、轨道半径为r。
有牛顿第二定律可得：
③ （1分）
小球恰能通过半圆轨道的最高点并沿轨道运动，有：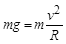
④（1分）
由③④联立得：
⑤（1分）
PO的最小距离为：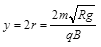
⑥ （1分）
即： （或）（1分）
（3）小球由O运动到N的过程中机械能守恒：mg·2R＋
mv2＝mv
⑦ （1分）
由④⑦得：
⑧ （1分）
根据运动的独立性可知，小球从N点进入电场区域后，在x轴方向以速度vN做匀速直线运动，沿电场方向做初速度为零的匀加速直线运动，则沿x轴方向有：x＝vNt⑨（1分）
沿电场方向有：z＝at2⑩ （1分） 
? （1分）
t时刻小球距N点：
（1分）
考点：牛顿第二定律，二力平衡，机械能守恒定律，平抛运动的知识等。
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
，磁场为水平方向（图中垂直纸面向外），磁感应强度大小为B；在第二象限分布着沿x轴正向的水平匀强电场，场强大小
。现将放在A点的带电小球由静止释放，则小球需经多少时间才能落到地面（小球所带的电量不变）？
圆孤轨道上由静止自A端滑下．整个装置处在方向互相垂直的匀强电场与匀强磁场中．已知E＝100 V/m，水平向右；B＝1T，方向垂直纸面向里．求：
）点，沿
轴正方向射入磁场区域I.（电子质量为m，电荷量为e）
位置射出，求电子在磁场I中运动的时间t.
同时垂直电场和磁场的方向射入时，恰不改变运动方向。若粒子射入时只有电场，可测得粒子穿过电场时沿竖直方向向上偏移6．4 cm；若粒子射人时只有磁场，则粒子束离开磁场时偏离原方向的距离是多少?不计粒子的重力。
从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域，磁场方向垂直纸面向外，粒子飞出磁场区域后，从b处穿过x轴进入场强为E、方向与x轴负方向成60°角斜向下的匀强电场中，速度方向与 x轴正方向的夹角为30°，经过一段时间后恰好通过b点正下方的c点，粒子的重力不计．试求：