题目内容
3.在抗洪抢险中,战士驾驶摩托艇救人.洪水沿平直的江岸向下游流去,水流速度为V1,摩托艇在静水中的航速为V2,战士救人的地点A离岸边最近处O的距离为d,下列有关说法中正确的是( )| A. | 战士将人送上岸的最短时间一定为$\frac{d}{{\sqrt{v_2^2-v_1^2}}}$ | |
| B. | 若战士在最短时间内将人送上岸,其登陆地点离O点的距离为$\frac{{d{v_1}}}{v_2}$ | |
| C. | 战士将人送上岸所通过的位移一定为d | |
| D. | 若战士驾驶的摩托艇的航向始终指向正对岸,其登陆地点一定是O点 |
分析 当摩托艇在静水中的速度方向垂直于河岸时,渡河时间最短,在垂直于河岸方向上由运动学公式可计算出所需的时间,继而可判知选项A的正误;此过程还要沿河岸向下游运动,由河水的速度与所用时间的乘积即可得知其登陆地点离O点的距离,再对位移进行合成,即可得知摩托艇的实际位移,继而得知选项BCD的正误;
解答 解:A、当摩托艇在静水的速度与河岸垂直时,渡河时间最短.此时时间为:t=$\frac{d}{{v}_{2}}$,所以选项A错误.
B、若战士在最短时间内将人送上岸,摩托艇在静水的速度应与河岸垂直,其登陆地点离O点的距离为s=v1×t=$\frac{{d{v_1}}}{v_2}$,所以选项B正确.
C、由B得解答可知,战士将人送上岸所通过的位移不一定为d,所以选项C错误.
D、若战士驾驶的摩托艇的航向始终指向正对岸,摩托艇还要沿河岸向下游运动,所以此种情况下,登陆地点在O点的下游.所以选项D错误.
故选:B
点评 该题通过渡河的模型考察了运动的合成与分解,关于渡河问题,应注意几种渡河方式,一是垂直渡河,此时渡河位移最短,但是所用时间不是最短的,此种情况要求船的合速度与河岸垂直,二是船头始终指向对岸的渡河,此种情况下渡河时间最短,但是渡河位移不是最短;关于渡河问题,还要会判断能否垂直渡河,其条件是船在静水中的速度大小要大于河水流动的速度大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图所示,放在水平地面上的光滑绝缘筒有两个带正电的小球A、B,A位于筒底靠左侧壁处,B在右侧筒壁上P处时处于平衡状态,现将B小球向上移动一段距离,从E处由静止开始释放,则在它下落到筒底前( )
如图所示,放在水平地面上的光滑绝缘筒有两个带正电的小球A、B,A位于筒底靠左侧壁处,B在右侧筒壁上P处时处于平衡状态,现将B小球向上移动一段距离,从E处由静止开始释放,则在它下落到筒底前( )
 如图所示,放在水平地面上的光滑绝缘筒有两个带正电的小球A、B,A位于筒底靠左侧壁处,B在右侧筒壁上P处时处于平衡状态,现将B小球向上移动一段距离,从E处由静止开始释放,则在它下落到筒底前( )
如图所示,放在水平地面上的光滑绝缘筒有两个带正电的小球A、B,A位于筒底靠左侧壁处,B在右侧筒壁上P处时处于平衡状态,现将B小球向上移动一段距离,从E处由静止开始释放,则在它下落到筒底前( )| A. | 小球A对筒底的压力保持不变 | B. | 小球B对筒壁的压力逐渐增大 | ||
| C. | 小球B的动能先增大后减小 | D. | 小球A、B间的电势能逐渐减小 |
8. 如图所示,一带负电的离子在某一正电荷Q形成的电场中,Q位于虚线MN上某处,离子只在电场力的作用下运动轨迹如图中实线所示,轨迹相对水平轴线MN对称,A,B,C为轨迹上的点,B点位于轨迹的最右端.以下说法中正确的是( )
如图所示,一带负电的离子在某一正电荷Q形成的电场中,Q位于虚线MN上某处,离子只在电场力的作用下运动轨迹如图中实线所示,轨迹相对水平轴线MN对称,A,B,C为轨迹上的点,B点位于轨迹的最右端.以下说法中正确的是( )
 如图所示,一带负电的离子在某一正电荷Q形成的电场中,Q位于虚线MN上某处,离子只在电场力的作用下运动轨迹如图中实线所示,轨迹相对水平轴线MN对称,A,B,C为轨迹上的点,B点位于轨迹的最右端.以下说法中正确的是( )
如图所示,一带负电的离子在某一正电荷Q形成的电场中,Q位于虚线MN上某处,离子只在电场力的作用下运动轨迹如图中实线所示,轨迹相对水平轴线MN对称,A,B,C为轨迹上的点,B点位于轨迹的最右端.以下说法中正确的是( )| A. | 正点电荷Q一定在B点左侧 | B. | 离子在B点的加速度一定最大 | ||
| C. | 离子在B点的动能可能最小 | D. | 离子在B点的电势能可能最小 |
13.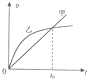 质量相等的甲乙两物体从离地面相同高度同时由静止开始下落,由于两物体的形状不同,运动中受到的空气阻力不同.将释放时刻作为t=0时刻,两物体的v-t图象如图所示.则下列判断正确的是( )
质量相等的甲乙两物体从离地面相同高度同时由静止开始下落,由于两物体的形状不同,运动中受到的空气阻力不同.将释放时刻作为t=0时刻,两物体的v-t图象如图所示.则下列判断正确的是( )
 质量相等的甲乙两物体从离地面相同高度同时由静止开始下落,由于两物体的形状不同,运动中受到的空气阻力不同.将释放时刻作为t=0时刻,两物体的v-t图象如图所示.则下列判断正确的是( )
质量相等的甲乙两物体从离地面相同高度同时由静止开始下落,由于两物体的形状不同,运动中受到的空气阻力不同.将释放时刻作为t=0时刻,两物体的v-t图象如图所示.则下列判断正确的是( )| A. | t0时刻之前,甲物体受到的空气阻力总是大于乙物体受到的空气阻力 | |
| B. | 甲物体在t0时刻的速度小于乙物体0-t0时间内的平均速度 | |
| C. | t0时刻甲乙两物体在同一高度 | |
| D. | 两物体不可能同时落地 |
 如图所示,M、N为两块水平放置的平行金属板,长为L,相距为2d,当S断开时(两板未充电),一带电量为+q,质量为m的油滴,以一水平初速度从两板间中点p飞入,恰好落到下板的中点Q处.求:
如图所示,M、N为两块水平放置的平行金属板,长为L,相距为2d,当S断开时(两板未充电),一带电量为+q,质量为m的油滴,以一水平初速度从两板间中点p飞入,恰好落到下板的中点Q处.求: 某压榨机的结构示意图如图所示,其中B为固定绞链,若在A铰链处作用一垂直于壁的力F,则由于力F的作用,使滑块C压紧物体D,设C与D光滑接触,杆的重力重力不计.压榨机的尺寸如图所示,求物体D所受压力的大小是F的多少倍?(滑块C重力不计)
某压榨机的结构示意图如图所示,其中B为固定绞链,若在A铰链处作用一垂直于壁的力F,则由于力F的作用,使滑块C压紧物体D,设C与D光滑接触,杆的重力重力不计.压榨机的尺寸如图所示,求物体D所受压力的大小是F的多少倍?(滑块C重力不计) 如图所示,一个匝数n=30的矩形线框可能垂直于磁场的轴OO′匀速转动,线圈面积为0.02m2,磁感应强度的大小B=2T,角速度ω=100rad/s.若从线圈经过中性面开始计时,试求:
如图所示,一个匝数n=30的矩形线框可能垂直于磁场的轴OO′匀速转动,线圈面积为0.02m2,磁感应强度的大小B=2T,角速度ω=100rad/s.若从线圈经过中性面开始计时,试求: