题目内容
 如图所示,一不可伸长的轻绳上端悬挂于O点,下端系一小球.现将小球拉到A点(保持绳绷直)由静止释放,当它经过最低点B时绳恰好被拉断,小球水平抛出后落到水平地面C点.已知B点离地高度为H,A、B两点的高度差为h,地面上的D点与OB在同一竖直线上.不计空气阻力,求:
如图所示,一不可伸长的轻绳上端悬挂于O点,下端系一小球.现将小球拉到A点(保持绳绷直)由静止释放,当它经过最低点B时绳恰好被拉断,小球水平抛出后落到水平地面C点.已知B点离地高度为H,A、B两点的高度差为h,地面上的D点与OB在同一竖直线上.不计空气阻力,求:(1)地面上DC两点间的距离s;
(2)小球落地时的速度vc.
分析:小球从A到B过程机械能守恒,从而可求解小球到B点的速度,小球从B到C做平抛运动,根据平抛运动规律可求解
解答:解:(1)小球从A到B过程机械能守恒,故mgh=
m
①
小球从B到C做平抛运动,在竖直方向上有:H=
gt2 ②
水平方向上有:s=vBt ③
由①②③式联立可得,s=2
(2)vy=gt=
故落地点的速度vc=
=
vc与水平方向夹角θ,tanθ=
=
=
答:(1)地面上DC两点间的距离为2
(2)小球落地时的速度为
,与水平方向夹角为arctan
.
| 1 |
| 2 |
| v | 2 B |
小球从B到C做平抛运动,在竖直方向上有:H=
| 1 |
| 2 |
水平方向上有:s=vBt ③
由①②③式联立可得,s=2
| Hh |
(2)vy=gt=
| 2gH |
故落地点的速度vc=
|
| 2g(h+H) |
vc与水平方向夹角θ,tanθ=
|
| ||
|
|
答:(1)地面上DC两点间的距离为2
| Hh |
(2)小球落地时的速度为
| 2g(h+H) |
|
点评:本题主要机械能守恒规律和平抛运动规律,知道平抛运动在水平方向是匀速直线运动,竖直方向上自由落地运动,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,一不可伸长的轻绳长为L,一端固定在O点,另一端系着一个质量为m 的小球.开始小球处于A点细绳恰好拉直(绳中无拉力),现让小球由静止自由释放,则小球运动到O正下方的C点时绳子的拉力大小为( )
如图所示,一不可伸长的轻绳长为L,一端固定在O点,另一端系着一个质量为m 的小球.开始小球处于A点细绳恰好拉直(绳中无拉力),现让小球由静止自由释放,则小球运动到O正下方的C点时绳子的拉力大小为( )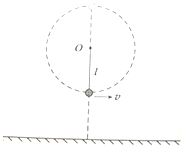 如图所示,一不可伸长的轻质细绳,绳长为L一端固定于O点,另一端系一质量为m的小球,小球绕O点在竖直平面内做圆周运动(不计空气助力),小球通过最低点时的速度为v.
如图所示,一不可伸长的轻质细绳,绳长为L一端固定于O点,另一端系一质量为m的小球,小球绕O点在竖直平面内做圆周运动(不计空气助力),小球通过最低点时的速度为v. 如图所示,一不可伸长的柔软轻绳跨过光滑的定滑轮,绳两端各系一小球a和b.a球质量为m,静置于地面;b球质量为3m,用手托住,高度为h,此时轻绳刚好拉紧.从静止开始释放b,则当b刚落地时a的速度为( )
如图所示,一不可伸长的柔软轻绳跨过光滑的定滑轮,绳两端各系一小球a和b.a球质量为m,静置于地面;b球质量为3m,用手托住,高度为h,此时轻绳刚好拉紧.从静止开始释放b,则当b刚落地时a的速度为( )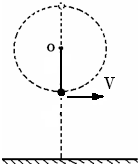 如图所示,一不可伸长的轻质细绳,绳长为L一端固定于O点,另一端系一质量为m的小球,小球绕O点在竖直平面内做圆周运动(不计空气助力),已知小球通过最低点时的速度为v,圆心0点距地面高度为h,重力加速度为g
如图所示,一不可伸长的轻质细绳,绳长为L一端固定于O点,另一端系一质量为m的小球,小球绕O点在竖直平面内做圆周运动(不计空气助力),已知小球通过最低点时的速度为v,圆心0点距地面高度为h,重力加速度为g