��Ŀ����
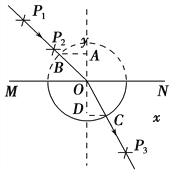
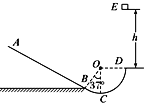
����Ŀ����ͼ��ʾ��ˮƽ���ʹ���5m/s���ٶ���˳ʱ�뷽���˶����ڴ��ʹ��ϵ�P������ط���һ����m��1 kg��С��飬PA��ľ���Ϊ1.5m��С����洫�ʹ��˶���A���ˮƽ�׳���ǡ����Բ�����ߴ�B�������ֱ�⻬Բ������˶���B��CΪԲ�������˵�������ˮƽ��CDΪ��C�����е�һ�̶�б�档С����뿪C���0.8 sͨ��D�㡣��֪С����봫�ʹ���Ķ�Ħ��������1��0.3��Բ�������͵�ΪO��A����ˮƽ��ĸ߶Ȳ�h��0.8 m��С�����б���Ķ�Ħ��������2��![]() ��sin 37��=0.6��cos 37��=0.8�� gȡ10 m/s2������
��sin 37��=0.6��cos 37��=0.8�� gȡ10 m/s2������

(1)С����뿪A��ʱ���ٶȴ�С��
(2)Բ��BOC��Ӧ��Բ�Ľ���Ϊ���٣�
(3)б����CD��ľ��롣
���𰸡���1��3m/s��2��1060 ��3��0.98m
��������
��1����С����P��Aȫ���ȼ��٣����ݶ��ܶ�����
��mgS1=![]()
���:v=3m/s< 5m/s ���С��鵽A��ʱ���ٶ�Ϊ3m/s
��2����С��飬��A��B��ƽ���˶���
![]()
��ã�vy=4m/s
![]()
����=1060
��3��С�����B�����ٶȣ�VB=![]() = 5m/s
= 5m/s
��е���غ�֪��![]()
С�����б���ϻ���![]()
С�����C��������ߵ㣺![]()
S1=![]() =1.25m
=1.25m
С�����б���»���![]()
С�������ߵ�ص�D�㣺 s2=![]() a2(t-t1)2=0.27m
a2(t-t1)2=0.27m
б����CD��ľ��룺SCD=S1-S2=0.98m

 ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�