Question

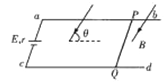
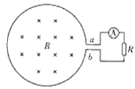
【题目】如图所示，金属圆环半径为L、电阻为r，金属环上有一个小缺口ab，用导线把金属环通过电流表接在电阻R两端，已知R=2r，电流表为理想电表。垂直于圆环面有一磁场，从t=0开始，磁感应强度随时间变化的规律为B=B0cos(ωt)，t=0时磁场垂直纸面向里，则下列说法正确的是

A. t=时，电流表示数一定不为0

B. t=时，a点电势低于b点

C. t=时，R两端电压为0

D. 从t=0到t=的过程中通过R的电荷量为q=

Answer 1

【答案】AD

【解析】

本题的关键是首先根据法拉第电磁感应定律，并结合“变化率”的概念，求出线圈中产生的感应电动势的表达式，然后进行推导讨论即可．

A、磁感应强度B=B0cos(ωt)，则由磁通量可得按余弦规律变化，则由知产生的瞬时电动势是按正弦规律变化的交流电 ，当时，即瞬时电流为零，但电流表测量的是正弦交流电的有效值为不为零；故A正确.

B、C、当时，，磁通量为负正在增大，则由楞次定律可知感应电流为顺时针，大小为，而线圈为感生电源，内部电流为，故；则B，C均错误.

D、根据电量的定义，从t=0到t=的过程中，则；故D正确.

故选AD.