题目内容
20.在地质、地震、勘探、气象和地球物理等领域的研究中,需要精确的重力加速度g值,g值可由实验精确测定.近年来测g值的一种方法叫“对称自由下落法”,它是将测g值归于测长度和时间,以稳定的氦氖激光的波长为长度标准,用光学干涉的方法测距离,以铷原子钟或其他手段测时间,此方法能将g值测得很准.具体做法是:将真空长直管沿竖直方向放置,自其中的O点向上抛小球,从抛出小球至小球又落回抛出点的时间为T2;小球在运动过程中经过比O点高H的P点,小球离开P点至又回到P点所用的时间为T1.由T1、T2和H的值可求得g等于( )| A. | $\frac{8H}{{{T}_{1}}^{2}-{{T}_{2}}^{2}}$ | B. | $\frac{4H}{{{T}_{2}}^{2}-{{T}_{1}}^{2}}$ | C. | $\frac{8H}{{{T}_{2}}^{2}-{{T}_{1}}^{2}}$ | D. | $\frac{H}{4{T}_{2}-{{T}_{1}}^{2}}$ |
分析 根据竖直上抛运动的对称性,求出小球从O点和P点到达最高点的时间,根据速度时间公式求出O和P点的速度,结合平均速度推论,抓住OP间的距离求出g值的大小.
解答 解:从抛出小球至小球又落回抛出点的时间为T2,根据竖直上抛运动的对称性,知小球到达最高点的时间为$\frac{{T}_{2}}{2}$,根据速度时间公式得,O点的速度${v}_{1}=g\frac{{T}_{2}}{2}$,
小球在运动过程中经过比O点高H的P点,小球离开P点至又回到P点所用的时间为T1.同理知小球从P点到达最高点的时间为$\frac{{T}_{1}}{2}$,根据速度时间公式得,P点的速度${v}_{2}=g\frac{{T}_{1}}{2}$,
根据平均速度推论知,H=$\frac{{v}_{1}+{v}_{2}}{2}(\frac{{T}_{2}}{2}-\frac{{T}_{1}}{2})$,
解得g=$\frac{8H}{{{T}_{2}}^{2}-{{T}_{1}}^{2}}$.
故选:C.
点评 对称自由落体法实际上利用了竖直上抛运动的对称性,所以解决本题的关键是将整个运动分解成向上的匀减速运动和向下匀加速运动,利用下降阶段即自由落体运动阶段解题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
10.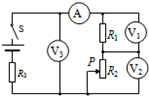 在如图所示电路中,闭合开关S,当滑动变阻器的滑片P 向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,各电表示数变化量的大小分别用△I、△U1、△U2和△U3表示.下列判断正确的是( )
在如图所示电路中,闭合开关S,当滑动变阻器的滑片P 向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,各电表示数变化量的大小分别用△I、△U1、△U2和△U3表示.下列判断正确的是( )
 在如图所示电路中,闭合开关S,当滑动变阻器的滑片P 向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,各电表示数变化量的大小分别用△I、△U1、△U2和△U3表示.下列判断正确的是( )
在如图所示电路中,闭合开关S,当滑动变阻器的滑片P 向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,各电表示数变化量的大小分别用△I、△U1、△U2和△U3表示.下列判断正确的是( )| A. | |△U1|+|△U2|<|△U3| | B. | |$\frac{{U}_{1}}{I}$|不变,|$\frac{△{U}_{2}}{△I}$|变大,|$\frac{△{U}_{3}}{△I}$|变大 | ||
| C. | |△U1|+|△U2|=|△U3| | D. | |$\frac{{U}_{2}}{I}$|变大,|$\frac{△{U}_{2}}{△I}$|不变,|$\frac{△{U}_{3}}{△I}$|不变 |
11.如图所示,水平长直轨道上两辆小车,甲车向左速度大小为v1,乙车向右的速度大小为v2,甲车上装有一支枪,每隔时间△t0水平射出一颗子弹,都能击中装在乙车上的靶子,不计子弹的重力和空气阻力,每颗子弹对地速度保持v0不变,每颗子弹中靶时,下一个子弹已经射出,设两车速度不受子弹射击的影响,随着时间的推移,可知( )


| A. | 空中相邻两颗子弹间的距离不变,且为(v0+v1)△t0 | |
| B. | 空中相邻两颗子弹间的距离会依次变大,因而不是定值 | |
| C. | 相邻两颗子弹中靶的时间间隔不变,且为$\frac{{({{v_0}-{v_2}})△{t_0}}}{{({{v_0}+{v_1}})}}$ | |
| D. | 相邻两颗子弹中靶的时间间隔不变,但不为$\frac{{({{v_0}-{v_2}})△{t_0}}}{{({{v_0}+{v_1}})}}$ |
15.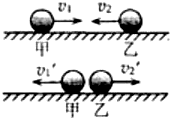 甲、乙两物体在光滑水平面上沿同一直线相向运动,甲、乙物体的速度大小分别为3m/s和1m/s;碰撞后甲、乙两物体都反向运动,速度大小均为1.5m/s.则甲、乙两物体质量之比为( )
甲、乙两物体在光滑水平面上沿同一直线相向运动,甲、乙物体的速度大小分别为3m/s和1m/s;碰撞后甲、乙两物体都反向运动,速度大小均为1.5m/s.则甲、乙两物体质量之比为( )
 甲、乙两物体在光滑水平面上沿同一直线相向运动,甲、乙物体的速度大小分别为3m/s和1m/s;碰撞后甲、乙两物体都反向运动,速度大小均为1.5m/s.则甲、乙两物体质量之比为( )
甲、乙两物体在光滑水平面上沿同一直线相向运动,甲、乙物体的速度大小分别为3m/s和1m/s;碰撞后甲、乙两物体都反向运动,速度大小均为1.5m/s.则甲、乙两物体质量之比为( )| A. | 2:3 | B. | 2:5 | C. | 3:5 | D. | 5:9 |
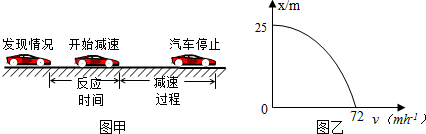
9.有一些关于运动学的概念和计算,其中正确的是( )
| A. | 为了简捷的研究物理问题,物理学引入了质点模型,质点实际上也存在 | |
| B. | 在本届秋季运动会4×100m的接力赛中,一(1)队取得了45.45s的好成绩,4位运动员的奔跑的平均速度约为8.8/s | |
| C. | 物体做匀变速直线运动,其加速度大小3m/s2,表示物体在任何1s内速度都增加3m/s | |
| D. | 一般讲平均速度时,必须讲清楚是哪段时间(或哪段位移)内的平均速度 |
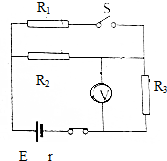 在如图电路中,电阻R1=R2=R3=1Ω,当S闭合时,电压表示数为1V,当S断开时,电压表示数为0.8V,试求电路中电源的电动势和内阻.
在如图电路中,电阻R1=R2=R3=1Ω,当S闭合时,电压表示数为1V,当S断开时,电压表示数为0.8V,试求电路中电源的电动势和内阻.