题目内容
10.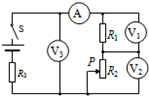 在如图所示电路中,闭合开关S,当滑动变阻器的滑片P 向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,各电表示数变化量的大小分别用△I、△U1、△U2和△U3表示.下列判断正确的是( )
在如图所示电路中,闭合开关S,当滑动变阻器的滑片P 向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,各电表示数变化量的大小分别用△I、△U1、△U2和△U3表示.下列判断正确的是( )| A. | |△U1|+|△U2|<|△U3| | B. | |$\frac{{U}_{1}}{I}$|不变,|$\frac{△{U}_{2}}{△I}$|变大,|$\frac{△{U}_{3}}{△I}$|变大 | ||
| C. | |△U1|+|△U2|=|△U3| | D. | |$\frac{{U}_{2}}{I}$|变大,|$\frac{△{U}_{2}}{△I}$|不变,|$\frac{△{U}_{3}}{△I}$|不变 |
分析 本题要分定值电阻与可变电阻去分析.对于定值电阻,有R=$\frac{U}{I}=\frac{△U}{△I}$;对于可变电阻,可根据闭合电路欧姆定律分析$\frac{△U}{△I}$与电源内阻的关系,从而作出判断.
解答 解:
AC、当滑动变阻器的滑片P向下滑动时,变阻器接入电路的电阻增大,电路中电流减小,则U1减小,内电压也减小,则U2增大,U3增大.
因为U1+U2=U3,则得△U1+△U2=△U3,因为△U1<0,△U2>0,△U3>0,所以|△U1|+|△U2|>|△U3|,故A、C错误.
BD、R1是定值电阻,则有R1=$\frac{{U}_{1}}{I}$=$\frac{△{U}_{1}}{△I}$,可知|$\frac{{U}_{1}}{I}$|、|$\frac{△{U}_{1}}{△I}$|都不变.当滑动变阻器的滑动触头P向下滑动时,R2变大,R2是可变电阻,$\frac{{U}_{2}}{I}$=R2,变大,根据闭合电路欧姆定律得:U2=E-I(R1+r),则知|$\frac{△{U}_{2}}{△I}$|=R1+r,不变.由U3=E-Ir,则|$\frac{△{U}_{3}}{△I}$|=r,不变,故B错误,D正确.
故选:D
点评 本题要注意对于定值电阻,是线性元件,有有R=$\frac{U}{I}=\frac{△U}{△I}$;对于非线性元件,R=$\frac{U}{I}$≠$\frac{△U}{△I}$;也可以结合电源的U-I图线分析.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
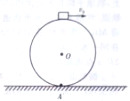
20.如图,在一半径为R的球面顶端放一质量为m的物块,A为球面底端的点,现给物块一初速度v0,则( )

| A. | 若v0=$\sqrt{gR}$,则物块落地点离A点距离为$\sqrt{2R}$ | |
| B. | 若球面是粗糙的,当v0<$\sqrt{gR}$时,物块一定会沿球面下滑一段 | |
| C. | 若v0<$\sqrt{gR}$,则物块落地点离A点距离为R | |
| D. | 若v0≥$\sqrt{gR}$,则物块落地点离A点至少为2R |
15. 一只松鼠静止地站在倾斜的树枝上,一只猴子从树枝上朝向右上方由静止跳出,则树枝对松鼠和猴子的弹力方向为( )
一只松鼠静止地站在倾斜的树枝上,一只猴子从树枝上朝向右上方由静止跳出,则树枝对松鼠和猴子的弹力方向为( )
 一只松鼠静止地站在倾斜的树枝上,一只猴子从树枝上朝向右上方由静止跳出,则树枝对松鼠和猴子的弹力方向为( )
一只松鼠静止地站在倾斜的树枝上,一只猴子从树枝上朝向右上方由静止跳出,则树枝对松鼠和猴子的弹力方向为( )| A. | 树枝对松鼠没有弹力 | B. | 树枝对松鼠弹力竖直向下 | ||
| C. | 树枝对猴子弹力垂直树干斜向上 | D. | 树枝对猴子弹力竖直向上 |
2.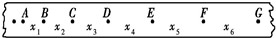 在研究速度与时间的关系的实验中,获得如图所示的纸带,A、B、C、D、E、F、G为计数点,相邻两计数点的时间间隔为T,x1、x2、x3、x4、x5、x6分别为AB、BC、CD、DE、EF、FG之间的距离,下列表达式中可以用来计算打D点时小车速度的有( )
在研究速度与时间的关系的实验中,获得如图所示的纸带,A、B、C、D、E、F、G为计数点,相邻两计数点的时间间隔为T,x1、x2、x3、x4、x5、x6分别为AB、BC、CD、DE、EF、FG之间的距离,下列表达式中可以用来计算打D点时小车速度的有( )
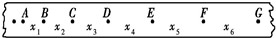 在研究速度与时间的关系的实验中,获得如图所示的纸带,A、B、C、D、E、F、G为计数点,相邻两计数点的时间间隔为T,x1、x2、x3、x4、x5、x6分别为AB、BC、CD、DE、EF、FG之间的距离,下列表达式中可以用来计算打D点时小车速度的有( )
在研究速度与时间的关系的实验中,获得如图所示的纸带,A、B、C、D、E、F、G为计数点,相邻两计数点的时间间隔为T,x1、x2、x3、x4、x5、x6分别为AB、BC、CD、DE、EF、FG之间的距离,下列表达式中可以用来计算打D点时小车速度的有( )| A. | $\frac{{x}_{2}+{x}_{4}}{T}$ | B. | $\frac{{x}_{2}+{x}_{3}+{x}_{4}+{x}_{5}}{4T}$ | ||
| C. | $\frac{{x}_{3}+{x}_{4}}{4T}$ | D. | $\frac{{x}_{2}+{x}_{4}}{2T}$ |
19.下列各装置中a点电势比b点电势高的有( )
| A. | 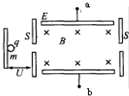 速度选择器 | B. | 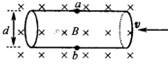 电磁流量计 | ||
| C. | 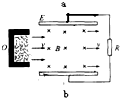 磁流体发电机 | D. | 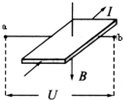 霍尔元件(金属板) |
20.在地质、地震、勘探、气象和地球物理等领域的研究中,需要精确的重力加速度g值,g值可由实验精确测定.近年来测g值的一种方法叫“对称自由下落法”,它是将测g值归于测长度和时间,以稳定的氦氖激光的波长为长度标准,用光学干涉的方法测距离,以铷原子钟或其他手段测时间,此方法能将g值测得很准.具体做法是:将真空长直管沿竖直方向放置,自其中的O点向上抛小球,从抛出小球至小球又落回抛出点的时间为T2;小球在运动过程中经过比O点高H的P点,小球离开P点至又回到P点所用的时间为T1.由T1、T2和H的值可求得g等于( )
| A. | $\frac{8H}{{{T}_{1}}^{2}-{{T}_{2}}^{2}}$ | B. | $\frac{4H}{{{T}_{2}}^{2}-{{T}_{1}}^{2}}$ | C. | $\frac{8H}{{{T}_{2}}^{2}-{{T}_{1}}^{2}}$ | D. | $\frac{H}{4{T}_{2}-{{T}_{1}}^{2}}$ |
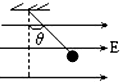 用一条绝缘轻绳悬挂一个带电小球,小球的质量为4.0×10-2kg,所带电荷量为+2.0×10-8C,现加一水平方向的匀强电场,平衡时绝缘绳与铅垂线成θ=600.求这个匀强电场的电场强度.
用一条绝缘轻绳悬挂一个带电小球,小球的质量为4.0×10-2kg,所带电荷量为+2.0×10-8C,现加一水平方向的匀强电场,平衡时绝缘绳与铅垂线成θ=600.求这个匀强电场的电场强度. 如图所示,质量为m的物体被三条同材质的绳子悬挂在O点,绳AO与水平方向的夹角为θ,绳BO水平,则:
如图所示,质量为m的物体被三条同材质的绳子悬挂在O点,绳AO与水平方向的夹角为θ,绳BO水平,则: