题目内容
如图所示,竖直平面内的3/4圆弧形光滑轨道半径为R,A端与圆心O等高,AD为水平面,B点为光滑轨道的最高点且在O的正上方,一个小球在A点正上方由静止释放,自由下落至A点进入圆轨道并恰好能通过B点,最后落到水平面C点处.求:
(1)释放点距A点的竖直高度;
(2)落点C到A点的水平距离.

(1)释放点距A点的竖直高度;
(2)落点C到A点的水平距离.
(1)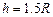
(2)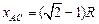
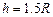
(2)
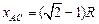
(1)小球恰能通过最高点B时,有:
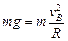 ,解得:
,解得: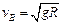 (3分)
(3分)
设释放点到A高度h,小球从释放到运动至B点的过程中,根据机械能守恒定律,有:
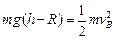 (3分)
(3分)
联立解得: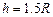 (2分)
(2分)
(2)小球从B到C做平抛运动,则
竖直分运动: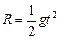 (2分)
(2分)
水平分运动: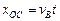 (2分)
(2分)
联立解得: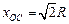 (2分)
(2分)
所以,落点C到A点的水平距离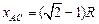 (1分)
(1分)
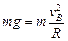 ,解得:
,解得: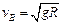 (3分)
(3分)设释放点到A高度h,小球从释放到运动至B点的过程中,根据机械能守恒定律,有:
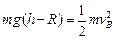 (3分)
(3分)联立解得:
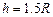 (2分)
(2分)(2)小球从B到C做平抛运动,则
竖直分运动:
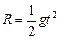 (2分)
(2分)水平分运动:
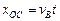 (2分)
(2分)联立解得:
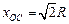 (2分)
(2分)所以,落点C到A点的水平距离
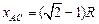 (1分)
(1分)
练习册系列答案
相关题目
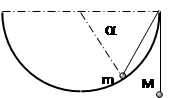

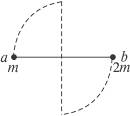
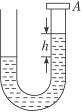
 能进行检测的一种高科技产物,现代汽车的生产也有运用风洞技术进行检测的,如图所示是小丽所在兴趣小组设计的一个类似于风洞的实验装置,他们在桌面上放有许多大小不同的塑料球,这些塑料球的密度均为
能进行检测的一种高科技产物,现代汽车的生产也有运用风洞技术进行检测的,如图所示是小丽所在兴趣小组设计的一个类似于风洞的实验装置,他们在桌面上放有许多大小不同的塑料球,这些塑料球的密度均为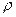 ,用水平向左恒定的风作用在球上,使它们做匀加速运动(摩擦不计)。已知风对球的作用力F与球的最大横截面积S成正比,即F=kS,走为一常量。对塑料球来说,可以认为空间存在一个风力场,在该风力场中风力对球做功与路径无关。 ( )
,用水平向左恒定的风作用在球上,使它们做匀加速运动(摩擦不计)。已知风对球的作用力F与球的最大横截面积S成正比,即F=kS,走为一常量。对塑料球来说,可以认为空间存在一个风力场,在该风力场中风力对球做功与路径无关。 ( )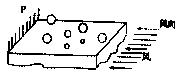
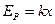
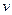 表示,风力场中机械能守恒定律可写为
表示,风力场中机械能守恒定律可写为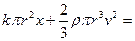 恒量
恒量
 恒( )
恒( )