Question

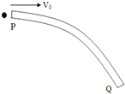
【题目】如图所示，P，Q是固定在竖直平面内的一段内壁光滑弯管的两端，P、Q间的水平距离为d.直径略小于弯管内径的小球以速度从P端水平射入弯管，从Q端射出，在穿过弯管的整个过程中小球与弯管无挤压。若小球从静止开始由P端滑入弯管，经时间t恰好以速度从Q端射出.重力加速度为g，不计空气阻力，那么( )

A.

B.

C.

D.

Answer 1

【答案】D

【解析】

以v0初速水平入射时，因小球与管壁无挤压，小球做平抛运动，水平方向应是匀速运动，竖直方向是自由落体运动，结合水平方向上的运动规律求出运动的时间，结合位移时间公式得出下降的高度，根据动能定理得出v0与d的关系．抓住小球静止释放时，水平方向上的平均速度小于v0得出运动时间．

以v0初速水平入射时，因小球与管壁无挤压，故水平方向应是匀速运动，竖直方向是自由落体运动，所以此时小球运动时间为：

下落高度为：

小球由静止开始运动时根据动能定理得：mgh=，则，解得：

以v0初速水平入射时，

当小球由静止释放时，水平方向平均速度一定小于v0，所以t＞t0

综上所述，故应选：D。