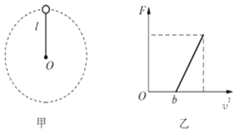题目内容
【题目】如图所示,A、B是水平传送带的两个端点,起初以![]() 的速度顺时针运转。今将一质量为1kg的小物块(可视为质点)无初速度地轻放在A处,同时传送带以
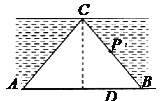
的速度顺时针运转。今将一质量为1kg的小物块(可视为质点)无初速度地轻放在A处,同时传送带以![]() 的加速度加速运转,物体和传送带间的动摩擦因素为0.2,水平桌面右侧有一竖直放置的光滑轨道CPN,其形状为半径R=0.8m的圆环剪去了左上角1350的圆弧,PN为其竖直直径,C点与B点的竖直距离为R,物体在B点水平离开传送带后由C点恰好无碰撞落入轨道。取g=10m/s2,求:
的加速度加速运转,物体和传送带间的动摩擦因素为0.2,水平桌面右侧有一竖直放置的光滑轨道CPN,其形状为半径R=0.8m的圆环剪去了左上角1350的圆弧,PN为其竖直直径,C点与B点的竖直距离为R,物体在B点水平离开传送带后由C点恰好无碰撞落入轨道。取g=10m/s2,求:

(1)物块由A端运动到B端所经历的时间。
(2)AC间的水平距离
(3)小物块在P点对轨道的压力。
【答案】(1)3s(2)8.6m(3)70-10![]() N
N
【解析】
试题(1)物体离开传送带后由C点无碰撞落入轨道,则得在C点物体的速度方向与C点相切,与竖直方向成45,有![]() ,
,
物体从B点到C作平抛运动,竖直方向:![]()
![]()
水平方向:![]()
得出![]()
![]()
物体刚放上传送带时,由牛顿第二定律![]() 得a=2m/s2
得a=2m/s2
物体历时t1后与传送带共速,则a t1=v0+ a0t1,t1=1s
得v1="2" m/s<4 m/s
故物体此时速度还没有达到vB,且此后的过程中由于![]() <
<![]() ,物体将和传送带以共同的加速度运动,设又历时t2到达B点 vB= v1+ a0t2
,物体将和传送带以共同的加速度运动,设又历时t2到达B点 vB= v1+ a0t2
得t2=2s
所以从A运动倒B的时间t= t1+t2=3s
AB间的距离s=![]() =7m
=7m
(2)从B到C的水平距离sBC=vBt3=2R=1.6m
所以A到C的水平距离sAC=s+sBC=8.6m
(3) 对CP段由动能定理![]()
对P点应牛顿第二定律:![]()
解得:N=70-10![]() N
N

【题目】某同学欲测量欧姆表“![]() ”档的内电阻和内部电源电动势。现有以下实验器材:
”档的内电阻和内部电源电动势。现有以下实验器材:
![]() :电流表
:电流表![]() ,
,![]()
![]() :电流表30mA,
:电流表30mA,![]()
![]() :电阻箱
:电阻箱![]()
![]() :滑动变阻器
:滑动变阻器![]()
电键、导线若干。
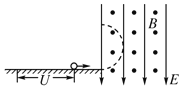
他利用电阻箱![]() 与电流表
与电流表![]() 串联接入图中电路。
串联接入图中电路。
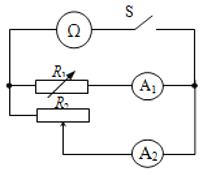
其电阻箱的阻值选择如图所示。
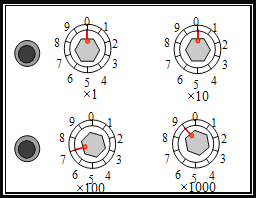
(1)闭合开关S,移动滑动变阻器的滑动端至某一位置,读出电流表![]() 和
和![]() 的示数
的示数![]() 和
和![]() 多次改变滑动端的位置,得到的数据为
多次改变滑动端的位置,得到的数据为
|
|
|
|
|
|
|
|
|
|
|
|
|
|
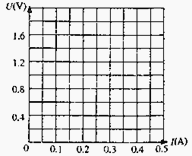
在图中所示的坐标纸上以![]() 为纵坐标、
为纵坐标、![]() 为横坐标画出所对应的
为横坐标画出所对应的![]() 曲线。
曲线。
(______________)
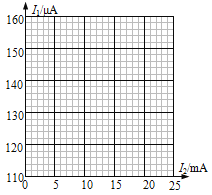
(2) 利用所得曲线求得欧姆表内电源的电动势![]() ______V,欧姆表内阻
______V,欧姆表内阻![]() ______
______![]() 。
。
(3) 将该欧姆表两个表笔短接,欧姆表的电流为![]() ______A。
______A。
【题目】在《描绘小灯泡伏安特性曲线》实验中选择“3V 0.5A的小灯泡作为研究对象,(填入器材序号)
A.电流表(量程0~0.6A,内阻1Ω)
B.电流表(量程0~3A,内阻1Ω)
C.电压表(量程0~15V,内阻约10kΩ)
D.电压表(0~3v,内阻约2kΩ)
E.滑动变阻器(阻值0~100Ω)
F.滑动变阻器(阻值0~10Ω)
G.电源E=6V
H.开关I,导线若干
(1)在本实验中,电流表应选择______电压表应选择______滑动变阻器应选择______
(2)滑动变阻器应采用______(填“分压”或“限流”)接法,电流表应采用______(填“内”、“外”)接法
(3)在答题卡虚线框中画出实验电路图. 可用的器材有:电压表、电流表、滑线变阻器(变化范围0—10Ω)、电源、小灯泡、电键、导线若干.(用直尺作图)______
(4)小灯泡灯丝的电阻会随温度的升高而变大.某同学为研究这一现象,用实验得到如下数据(I和U分别表示小灯泡上的电流和电压):
I(A) | 0.12 | 0.21 | 0.29 | 0.34 | 0.38 | 0.42 | 0.45 | 0.47 | 0.49 | 0.50 |
U(V) | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 | 2.00 |
在答题卡坐标格中画出小灯泡的U—I曲线保留描点痕迹)______