题目内容
如图所示,左边是一足够长的固定光滑曲面AB,其底端B的切线水平,B点与水平传送带的左端刚好平齐接触,传送带的长度L=5m,沿逆时针方向以恒定速度υ=2m/s匀速转动.CD为光滑的水平轨道,C点与传送带的左端刚好平齐接触,DE是竖直放置的半径为R=0.4m的光滑半圆轨道,DE与CD相切于D点.一个质量为m=1kg的物块(可视为质点)与传送带间的动摩擦因数μ=0.2,取g=10m/s2.
(1)若物块从曲面AB上距B点高为h=0.8m处由静止开始下滑,通过计算判断物块能否到达C点;
(2)若物块从曲面AB上距B点高为H处由静止开始下滑,能够通过C点,并经过圆弧轨道DE,从其最高点E飞出,最终落在CD上距D点的距离为x=1.2m处,求:
①物块通过E点时受到的压力大小;
②高度H.

(1)若物块从曲面AB上距B点高为h=0.8m处由静止开始下滑,通过计算判断物块能否到达C点;
(2)若物块从曲面AB上距B点高为H处由静止开始下滑,能够通过C点,并经过圆弧轨道DE,从其最高点E飞出,最终落在CD上距D点的距离为x=1.2m处,求:
①物块通过E点时受到的压力大小;
②高度H.

分析:(1)物块从h出下滑到底端时有机械能守恒求出到达B点时的速度,当滑上传送带时将做减速运动,速度减到零时求出滑行的位移与传送的长度比较即可;
(2)物块从E点做平抛运动,有平抛运动特点求出E点速度,由牛顿第二定律求出物块对轨道的压力;在整个过程中利用动能定理求出高度H.
(2)物块从E点做平抛运动,有平抛运动特点求出E点速度,由牛顿第二定律求出物块对轨道的压力;在整个过程中利用动能定理求出高度H.
解答:解:(1)由A到B的过程中由机械能守恒可知:
mgh=
解得:v1=
=
m/s=4m/s
滑块滑上传送带后后做减速运动由牛顿第二定律可知:
-μmg=ma
解得:a=-μg=-0.2×10m/s2=-2m/s2
当速度v2=0时到达向右的最大位移为x1
=2ax1
解得:x1=
=
m=4m<L
故物体不能到达C点
(2)①从E点做平抛运动,设E点的速度为v3
2R =
gt2
x=v3t
联立以上两式解得v3=3m/s
mg+N=m
N=m
-mg=1×
-1×10N =12.5N
②从开始下滑到E点的全程由动能定理
mgH-μmgL-mg?2R=
H=μL+2R+
=0.2×5+2×0.4+
m=2.25m
答:(1)通过计算判断物块不能到达C点;
(2)①物块通过E点时受到的压力大小为12.5N;
②高度H为2.25m.
mgh=
| 1 |
| 2 |
| mv | 2 1 |
解得:v1=
| 2gh |
| 2×10×0.8 |
滑块滑上传送带后后做减速运动由牛顿第二定律可知:
-μmg=ma
解得:a=-μg=-0.2×10m/s2=-2m/s2
当速度v2=0时到达向右的最大位移为x1
| v | 2 2 |
| -v | 2 1 |
解得:x1=
| ||
| 2a |
| -42 |
| 2×(-2) |
故物体不能到达C点
(2)①从E点做平抛运动,设E点的速度为v3
2R =
| 1 |
| 2 |
x=v3t
联立以上两式解得v3=3m/s
mg+N=m
| v23 |
| R |
N=m
| ||
| R |
| 32 |
| 0.4 |
②从开始下滑到E点的全程由动能定理
mgH-μmgL-mg?2R=
| 1 |
| 2 |
| mv | 2 3 |
H=μL+2R+
| ||
| 2g |
| 32 |
| 2×10 |
答:(1)通过计算判断物块不能到达C点;
(2)①物块通过E点时受到的压力大小为12.5N;
②高度H为2.25m.
点评:本题关键明确滑块的运动规律,然后分阶段运用牛顿第二定律、运动学公式、动能定理列式求解,较难.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
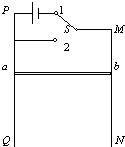 (2004?南汇区一模)如图所示,MNPQ是一个足够长的处于竖直平面内的固定的金属框架,框架的宽度为L,电阻忽略不计.ab是一根质量为m,有一定电阻的导体,能紧贴框架无摩擦下滑,整个框架平面处于垂直于框架平面的匀强磁场中,磁感强度为B.当单刀双掷开关S置于1位置时,导体ab恰好静止在框架的某一处.已知电源的电动势为ε,内阻为r.
(2004?南汇区一模)如图所示,MNPQ是一个足够长的处于竖直平面内的固定的金属框架,框架的宽度为L,电阻忽略不计.ab是一根质量为m,有一定电阻的导体,能紧贴框架无摩擦下滑,整个框架平面处于垂直于框架平面的匀强磁场中,磁感强度为B.当单刀双掷开关S置于1位置时,导体ab恰好静止在框架的某一处.已知电源的电动势为ε,内阻为r. 如图所示,MN是一根长为l=10cm,质量m=50g的金属棒,用两根长度也为l的细软导线将导体棒MN水平吊起,使导体棒处在B=
如图所示,MN是一根长为l=10cm,质量m=50g的金属棒,用两根长度也为l的细软导线将导体棒MN水平吊起,使导体棒处在B=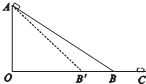 如图所示,ABC是一条长轨道,斜面和水平面摩擦因素相同,一质量为m的木块(可视为质点),在A点由静止释放,最后停在C点;现在改变斜面的倾角,如图中虚线AB'所示,仍从A点由静止释放该小木块,则木块最终将停放在(不计木块通过转折点B点或B'点的能量损失)( )
如图所示,ABC是一条长轨道,斜面和水平面摩擦因素相同,一质量为m的木块(可视为质点),在A点由静止释放,最后停在C点;现在改变斜面的倾角,如图中虚线AB'所示,仍从A点由静止释放该小木块,则木块最终将停放在(不计木块通过转折点B点或B'点的能量损失)( ) 如图所示,ABCD是一条长轨道,其中AB段是倾角为θ光滑斜面,A点离地高h=20m,CD段是水平的,物块与水平面间的动摩擦因数为μ=0.4,BC是与AB和CD都相切的一段光滑圆弧,其长度可忽略不计.一质量为m=1kg的小物块在A点从静止滑下,最后停在D点,求:
如图所示,ABCD是一条长轨道,其中AB段是倾角为θ光滑斜面,A点离地高h=20m,CD段是水平的,物块与水平面间的动摩擦因数为μ=0.4,BC是与AB和CD都相切的一段光滑圆弧,其长度可忽略不计.一质量为m=1kg的小物块在A点从静止滑下,最后停在D点,求: