题目内容
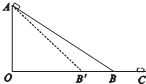如图所示，ABC是一条长轨道，斜面和水平面摩擦因素相同，一质量为m的木块（可视为质点），在A点由静止释放，最后停在C点；现在改变斜面的倾角，如图中虚线AB'所示，仍从A点由静止释放该小木块，则木块最终将停放在（不计木块通过转折点B点或B'点的能量损失）（ ）分析：通过对A点释放到停止全过程运用动能定理，判断在水平面上的位移是否发生变化来确定小木块停止的位置．
解答：解：设A距离地面的高度为h，动摩擦因数为μ，斜面的倾角为θ，对全过程运用动能定理有，mgh-μmgcosθs1-μmgs2=0，整理得：mgh-μmg（s1cosθ+s2）=0，而s1cosθ+s2等于OC的长度．与倾角无关，故停放的位置不变．故B正确，A、C、D错误．
故选B．
故选B．
点评：解决本题的关键会合理地选择研究的过程，即选择全过程为研究过程，运用动能定理求解．
练习册系列答案
相关题目
如图所示，ABC是一雪道，AB段为长L=80m倾角θ=37°的斜坡，BC段水平，AB与BC平滑相连．一个质量m=75kg的滑雪运动员，从斜坡顶端以v0=2.0m/s的初速度匀加速滑下，经时间t=5.0s 到达斜坡底端B点．滑雪板与雪道间的动摩擦因数在AB段和BC段均相同．取g=10m/s2．（sin37°=0.6，cos37°=0.8）．求：
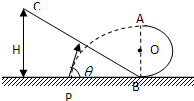如图所示，ABC是一条由半圆和一段斜面组成的光滑轨道，A、B两点在同一竖直线上，且已知半圆半径为R，今在水平面某一点P处抛出一个小球，使它恰好从A点进入轨道，在B点处无能量损失，最后沿斜面上升到高度为H处，试求小球抛出点P的位置，抛射速度V及抛射角θ
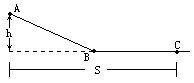如图所示，ABC是一条滑道，滑雪者从A点由静止开始沿倾斜滑道AB滑下，然后又沿水平滑道BC滑行，最后停在C点．已知A点距水平面的高度为h，A点跟C点间的水平距离为s．试证明：滑雪板跟滑道间的动摩擦因数μ＝h/s．
(不计空气阻力)。