题目内容
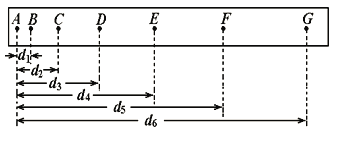
【题目】某校校园文化艺术节举行四驱车模型大赛,其中规定赛道如图所示.某四驱车以额定功率20 W在水平轨道AB处由静止开始加速4 s后从B点水平飞出,无碰撞进入圆弧轨道CD,该圆弧圆心角为37°,半径R0=5 m,竖直圆轨道的半径R=2.4 m.在恰好经过第一个圆弧轨道最高点F后,继续沿着轨道运动后从最高点H处水平飞出后落入沙坑中.已知沙坑距离EG平面高度为h2=2 m,四驱车的总质量为2 kg,g=10 m/s2(四驱车视为质点,C点以后轨道均视为光滑轨道).求:
(1)四驱车在水平轨道AB处克服摩擦力做功的大小;
(2)四驱车在E点对轨道的压力;
(3)末端平抛高台h1为多少时能让四驱车落地点距离G点水平位移最大,通过计算说明.

【答案】(1)16 J (2)120 N (3)2m
【解析】
(1)设AB阶段,设摩擦力做功为Wf ,根据动能定理得
Pt+Wf=![]() mvB2
mvB2
对四驱车在C点分析,如图所示.
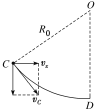
由于无碰撞从C点进入圆弧轨道,由几何关系(如图所示)得
vx=vB=vCcos 37°
根据机械能守恒定理得
![]() mvC2+mgR0(1-cos 37°)=
mvC2+mgR0(1-cos 37°)=![]() mvF2+2mgR
mvF2+2mgR
由于四驱车恰好经过最高点F,即
mg=m![]()
联立以上各式解得:
vC=10 m/s,vB=8 m/s,
Wf=-16 J,即克服摩擦力做功16 J.
(2)根据机械能守恒定理得:
![]() mvC2+mgR0(1-cos 37°)=
mvC2+mgR0(1-cos 37°)=![]() mvE2
mvE2
FN-mg=m![]()
代入数据得:FN=120N,由牛顿第三定律可知小车对轨道压力为120 N,方向竖直向下.
(3)根据机械能守恒定律得
![]() mvE2=mgh1+
mvE2=mgh1+![]() mvH2
mvH2
四驱车从H处飞出后做平抛运动,所以
h1+h2=![]() gt′2
gt′2
水平位移
x=vHt′
化简得:
x=![]() ·
·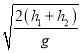
即
x=![]()
当h1=2 m,有水平最大距离,xmax=8 m.

练习册系列答案
相关题目