Question

【题目】如图所示，一质子源位于P点，该质子源在纸面内各向均匀地发射N个质子。在P点下方放置有长度L=1.2m以O为中点的探测板，P点离探测板的垂直距离OP为a。在探测板的上方存在方向垂直纸面向里，磁感应强度大小为B的匀强磁场。已知质子电荷量q=1.60×1019C，质子的质量与速度的乘积mv=4.8×10-21kg·m·s1（不考虑粒子之间的相互作用)。求

（1）当a=0.15m，B=0.1T时，求计数率(即打到探测板上质子数与总质子数N的比值)；

（2）若a取不同的值，可通过调节B的大小获得与（1）问中同样的计数率，求B与a的关系并给出B的取值范围。

Answer 1

【答案】(1)；(2) ，

【解析】

(1) 根据牛顿第二定律，有，得质子运动半径：

如图所示

轨迹与AB相切时落点最远，设质子与竖直方向的发射角为α时在O点左侧相切，发射角为β时在O点右侧相切，根据几何关系知，打到探测板对应发射角度：

能够打在AB板的夹角为：

可得质子计数率为：

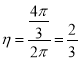
(2) 在确保计数率为的情况下，R'=2a，即，如图所示

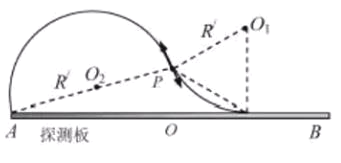
恰能打到探测板左端的条件为

即