��Ŀ����
����Ŀ����ͼ��ʾ��MNΪƽ�н����壬N������һС��Q��һ������ԴP��M�帽�������ͷų��ٶ�Ϊ�㣬����Ϊm�������Ϊq�Ĵ���������ӣ����Ӿ������ٵ糡���ٺ�С��Q������ذ뾶ΪR��ԲͲ�ϵ�С��E����ԲͲ��Ͳ����ƽ����Ͳ�����������ǿ�ų����ų��ĴŸ�Ӧǿ��ΪB��Ͳ����һС��F��С��E��Q��P��ͬһֱ���ϣ���ֱ����ų���ֱ��E��F����ΪͲ��ֱ�������ӽ���Ͳ�ڴų�ƫת����Ͳ����ײ���ٶȴ�С���䣬�����������ӵ�������
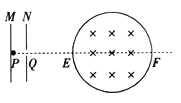
(1)Ҫʹ�������ٶ�v����ų���M��N��ĵ�ѹΪ���?
(2)��������Ͳ����ײһ�κ��F������������ڴų����˶���ʱ��Ϊ����?
(3)�����Ӵ�E�����ų�����Ͳ�ڷ���������ײ���F��������������ڴų����˶���·��Ϊ����?(��֪tan22.5��=![]() )
)
���𰸡���1��![]() ��2��
��2��![]() (3)
(3)![]()
����������1�����Ӿ����ٵ糡���٣����ݶ��ܶ����У�![]()
��ü��ٵ�ѹ�Ĵ�С![]()
��2����������Ͳ����ײһ�κ��F������ų������˶��켣��ͼ��ʾ��
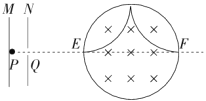
�����ڴų����˶���ʱ����������ڴų�����Բ���˶��İ�����ڣ�����
![]() ��
��![]()
������ã�![]()
��3�������ӽ���ų�����Ͳ�ڷ���������ײ���F��������������
�ٹ켣��ͼ��ʾ��

���ݼ��ι�ϵ���������ڴų�����Բ���˶��Ĺ켣�뾶![]()
�������ڴų����˶���·��![]()
�ڹ켣��ͼ��ʾ��
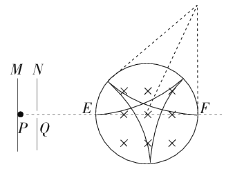
���ݼ��ι�ϵ���������ڴų�����Բ���˶��Ĺ켣�뾶![]()
�������ڴų����˶���·��![]()