Question

（2006?永州模拟）在光滑水平面上有一个静止的质量为M的木块，一颗质量为m的子弹以初速v0水平射入木块，且陷入木块的最大深度为d．设冲击过程中木块的运动位移为s，子弹所受阻力恒定．试证明：s＜d．

Answer 1

分析：由动量守恒的条件可知系统总动量守恒；分别对M、m由动能定理可得出s与d的关系．

解答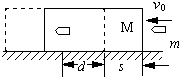：解：如图所示，
m冲击M的过程，m、M组成的系统水平方向不受外力，动量守恒mv₀=（m+M）v
设子弹所受阻力的大小为F，由动能定理得：
对M：Fs=

1

2

Mv2-0（3分）
对m：-F(s+d)=

1

2

mv2-

1

2

m

v

2 0

联立上式解得：s=

m

M+m

d
因

m

M+m

＜1，所以s＜d．

点评：本题为动量定恒与动能定理的结合题目，注意在解题中应灵活选取研究对象，应用动量定恒或动能定理列式求解．