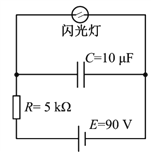
题目内容
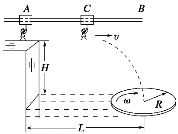
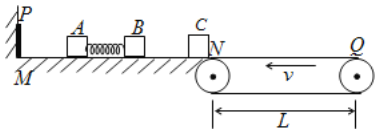
【题目】如图所示,光滑水平面MN左端有一固定弹性挡板P(物体与挡板碰撞时无能量损失),右端N与处于同一高度的水平传送带之间的间隙可忽略,传送带以![]() 的速度逆时针匀速转动。MN上放置着三个可视为质点的物体A、B和C,质量分别为mA=4kg、mB=1kg、mC=1kg,开始时,A、B静止,AB间有一个锁定的被压缩的轻质弹簧,弹性势能EP=40J,物体C静止在N点。现解除锁定,A、B被弹开后迅速移走弹簧,B和C相碰后粘在一起。A、B、C三个物体与传送带间的动摩擦因数均为μ=0.2,g=10m/s2。求:
的速度逆时针匀速转动。MN上放置着三个可视为质点的物体A、B和C,质量分别为mA=4kg、mB=1kg、mC=1kg,开始时,A、B静止,AB间有一个锁定的被压缩的轻质弹簧,弹性势能EP=40J,物体C静止在N点。现解除锁定,A、B被弹开后迅速移走弹簧,B和C相碰后粘在一起。A、B、C三个物体与传送带间的动摩擦因数均为μ=0.2,g=10m/s2。求:
(1)物体A、B被弹开时各自速度的大小;
(2)要使A与BC能在水平面MN上发生相向碰撞,则传送带NQ部分的长度L至少多长;
(3)若传送带NQ部分长度等于(2)问中的最小值,物体A与BC碰撞后结合成整体,此整体从滑上传送带到第一次离开传送带的过程中,系统有多少机械能转化成内能。
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)A、B被弹簧弹开的过程实际是爆炸模型,符合动量守恒、AB及弹簧组成的系统机械能守恒;
(2)B与C碰撞的过程中动量守恒,由此求出碰撞后的速度;对BC,运用用动能定理可以求出传送带NQ部分的长度;
(3)我们用逆向思维考虑:A、B整体最后刚好从Q点滑出那么它的末速度一定为零,即他们一直做匀减速运动,则A、B碰撞后的公共速度可求;而碰撞前B的速度已知,那么碰撞前A的速度利用动量守恒可求;既然A的速度求出来了,利用功能关系即可求出系统有多少机械能转化成内能;
(1)A、B物块被弹簧弹开的过程中,取向右为正方向,由动量守恒定律得:![]()
由能量守恒知:![]()
解得:![]() ,
,![]() ;
;
(2)B与C碰撞的过程中动量守恒,选取向右为正方向,则:![]()
代入数据得:![]()
要使三物块能在水平面MN上发生碰撞,小物块BC不能在传送带的Q端掉下,则小物块BC在传送带上至多减速运动达Q处。
以BC物块为研究对象,滑到最右端时速度为0,据动能定理有:![]()
解得:![]() ;
;
(3)传送带的速度小于![]() ,可知物块BC返回过程先加速后匀速,到达水平面MN上时的速度等于传送带速度大小,故
,可知物块BC返回过程先加速后匀速,到达水平面MN上时的速度等于传送带速度大小,故![]()
若两物块A、BC在水平面MN上相向碰撞结合成整体,设共同速度为![]() ,根据动量守恒有:
,根据动量守恒有:![]()
解得:![]() ,方向向右。
,方向向右。
因![]() ,所以三物块组成的整体滑上传送带后先向右减速,再向左加速回到水平面MN上,且速度与
,所以三物块组成的整体滑上传送带后先向右减速,再向左加速回到水平面MN上,且速度与![]() 等值。
等值。
整体与弹性挡板碰撞后再滑上传送带,如此重复运动。
三物块第一次在传送带上向右运动的过程中的加速度:![]()
物块向右运动的时间:![]()
相对传送带运动的距离为:![]()
物块向左加速的过程中相对于传送带的位移:![]()
故从整体第一次离开传送带的过程中,系统的机械能转化成内能大小为: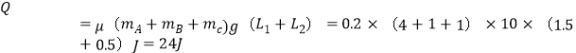 。
。

 目标测试系列答案
目标测试系列答案