Question

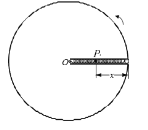
【题目】如图所示，一个理想边界为PQ、MV的足够大的匀强磁场区域，宽度为d，磁场方向垂直纸面向里。O点处有一体积可忽略的电子发射装置，能够在纸面所在平面内向磁场内各个方向连续、均匀地发射速度大小相等的电子，当电子发射速率为v0时，所有电子恰好都不能从MN边界射出磁场，则当电子发射速率为4v0时（　　）

A. 电子的运动半径为4d

B. 从MN边界射出的电子数占总电子数的三分之二

C. MN边界上有电子射出的总长度为2d

D. 电子在磁场中运动的最长时间为

Answer 1

【答案】BC

【解析】

根据左手定则判断电子所受的洛伦兹力方向，即可确定偏转方向；分析临界点，画出轨迹，由几何知识求出电子打在MN上的点与B点的距离以及转过的圆心角；确定出轨迹对应的圆心角，由圆周运动公式求解时间。

向磁场内各个方向连续、均匀地发射速度大小相等的电子，当电子发射速率为v0时，所有电子恰好都不能从MN边界射出磁场，则知r=d，则当电子发射速率为4v0时，根据r=知半径变为原来的4倍，即为2d，故A错误；

水平向右射出的粒子达到MN最右端的，r=2d，根据几何关系知偏折角为60°，AB=2dsin60°=d，与MN相切是到达的最左的点，根据几何关系知速度与PQ夹角为60°，所以从MN边界射出的电子数占总电子数的三分之二，BC=2dsin60°=d，MN边界上有电子射出的总长度为2d，故BC正确；根据BC项分析，转过的圆心角最大为60°，最长时间为，故D错误。故选BC。