Question

【题目】如图所示，“旋转秋千”中的两个座椅A、B质量相等，通过相同长度的缆绳悬挂在旋转圆盘上。不考虑空气阻力的影响，当旋转圆盘绕竖直的中心轴匀速转动时，下列说法正确的是（　　）

A.A的速度比B的小

B.A与B的向心加速度大小相等

C.悬挂A、B的缆绳与竖直方向的夹角相等

D.悬挂A的缆绳所受的拉力比悬挂B的小

Answer 1

【答案】AD

【解析】

如图所示

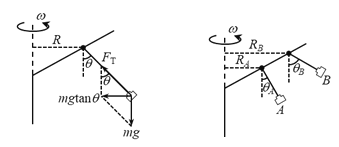
设转轴到悬挂点的距离为R，缆绳长为L，缆绳与竖直方向的夹角为θ，缆绳拉力与重力的合力提供向心力，由牛顿第二定律得

解得

当角速度ω、缆绳长L不变时，角度θ从0到90°逐渐增大，R也随着增大，因为A、B座椅同轴转动，所以它们的角速度ω相等，又因为A、B座椅缆绳长度L相同，且RA<RB，所以θA <θB。

AB．根据A、B座椅同轴转动可推知它们转动的角速度ω相等，且A座椅做圆周运动的半径RA +LsinθA比较小，由

v=ωr

可知A座椅的速度比B座椅的速度小，又由

a=ω2r

可知A座椅的向心加速度比B座椅的向心加速度小，故A正确，B错误；

C．由过程分析可知，悬挂A的缆绳与竖直方向的夹角比B的小，故C错误；

D．由过程分析可知，悬挂A、B的缆绳所受的拉力分别为

，

因为0 <θA <θB <90°，所以FTA <FTB，故D正确。

故选AD。