题目内容
19.做自由落体运动的物体,它在第1s内的平均速度是5m/s,在第1s内通过的路程是5m,它在第2s末的瞬时速度是20m/s,它在第5内的平均速度是45m/s,它在5s内的位移是45m.分析 自由落体运动做初速度为零的匀加速直线运动,根据位移时间公式求出第1s内的位移、前2s内的位移,以及第2s内的位移.
解答 解:由位移公式:第1s内通过的位移${x}_{1}=\frac{1}{2}g{{t}_{1}}^{2}=\frac{1}{2}×10×1m=5m$,它在第1s内的平均速度是:$\overline{{v}_{1}}=\frac{{x}_{1}}{{t}_{1}}=\frac{5}{1}=5$m/s
由速度公式:v=gt2=10×2=20m/s
前5s内的位移:${x}_{2}=\frac{1}{2}g{t}_{2}^{2}=\frac{1}{2}×10×{5}^{2}=125m$
前4s内的位移:${x}_{4}=\frac{1}{2}g{t}_{4}^{2}=\frac{1}{2}×10×{4}^{2}=80m$,
则第5s内的位移△x=x2-x4=125-80m=45m.
第5s内的平均速度:$\overline{{v}_{5}}=\frac{△x}{△t}=\frac{45}{1}=45$m/s
故答案为:5,5,20,45,45.
点评 解决本题的关键知道自由落体运动的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
7.下列各实例中,属于机械能守恒的是( )
①做自由落体运动的小球
②跳伞员带着张开的降落伞匀速下降
③小球沿光滑圆弧槽滑下
④用不计质量的细棒一端拴一小球另一端固定,使小球绕固定点在竖直平面内作匀速圆周运动.
①做自由落体运动的小球
②跳伞员带着张开的降落伞匀速下降
③小球沿光滑圆弧槽滑下
④用不计质量的细棒一端拴一小球另一端固定,使小球绕固定点在竖直平面内作匀速圆周运动.
| A. | ①② | B. | ①③ | C. | ②③ | D. | ③④ |
4.一个做初速度为0的匀加速直线运动的物体,它在前4s内通过的位移是16m,则它的加速度为( )
| A. | 0.5 m/s2 | B. | 1 m/s2 | C. | 1.5 m/s2 | D. | 2 m/s2 |
11. 如图所示为大型电子地磅电路图,所用器材均为理想器材,电源电动势为E,内阻不计,不称物体时,滑片P在A端,滑动变阻器接入电路的有效电阻最大,电流较小;称重物时在压力作用下使滑片P下滑,滑动变阻器有效电阻变小,电流变大,这样把电流对应的重量值刻在刻度盘上,就可以读出被称物体的重量值.若滑动变阻器上A、B间距离为L,最大阻值等于电阻阻值R0,己知两只弹簧的总弹力与形变量成正比,比例系数为k,下列说法正确的是( )
如图所示为大型电子地磅电路图,所用器材均为理想器材,电源电动势为E,内阻不计,不称物体时,滑片P在A端,滑动变阻器接入电路的有效电阻最大,电流较小;称重物时在压力作用下使滑片P下滑,滑动变阻器有效电阻变小,电流变大,这样把电流对应的重量值刻在刻度盘上,就可以读出被称物体的重量值.若滑动变阻器上A、B间距离为L,最大阻值等于电阻阻值R0,己知两只弹簧的总弹力与形变量成正比,比例系数为k,下列说法正确的是( )
 如图所示为大型电子地磅电路图,所用器材均为理想器材,电源电动势为E,内阻不计,不称物体时,滑片P在A端,滑动变阻器接入电路的有效电阻最大,电流较小;称重物时在压力作用下使滑片P下滑,滑动变阻器有效电阻变小,电流变大,这样把电流对应的重量值刻在刻度盘上,就可以读出被称物体的重量值.若滑动变阻器上A、B间距离为L,最大阻值等于电阻阻值R0,己知两只弹簧的总弹力与形变量成正比,比例系数为k,下列说法正确的是( )
如图所示为大型电子地磅电路图,所用器材均为理想器材,电源电动势为E,内阻不计,不称物体时,滑片P在A端,滑动变阻器接入电路的有效电阻最大,电流较小;称重物时在压力作用下使滑片P下滑,滑动变阻器有效电阻变小,电流变大,这样把电流对应的重量值刻在刻度盘上,就可以读出被称物体的重量值.若滑动变阻器上A、B间距离为L,最大阻值等于电阻阻值R0,己知两只弹簧的总弹力与形变量成正比,比例系数为k,下列说法正确的是( )| A. | 所称重物的重量G与电流大小I的关系为G=2kL-$\frac{EkL}{I{R}_{0}}$ | |
| B. | 若满偏电流为I0,則满偏位置刻重量值为G=2kL+$\frac{EkL}{{I}_{0}{R}_{0}}$ | |
| C. | 重量值的零刻线刻在电流表$\frac{E}{2{R}_{0}}$处 | |
| D. | 增大电流表量程会减小装置的测量精度 |
8.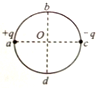 如图所示,真空中有一个半径为r的圆,圆心为O,直径ac、bd相互垂直,在a、c处分别固定有电荷量为+q、-q的两个点电荷.下列说法正确的是( )
如图所示,真空中有一个半径为r的圆,圆心为O,直径ac、bd相互垂直,在a、c处分别固定有电荷量为+q、-q的两个点电荷.下列说法正确的是( )
 如图所示,真空中有一个半径为r的圆,圆心为O,直径ac、bd相互垂直,在a、c处分别固定有电荷量为+q、-q的两个点电荷.下列说法正确的是( )
如图所示,真空中有一个半径为r的圆,圆心为O,直径ac、bd相互垂直,在a、c处分别固定有电荷量为+q、-q的两个点电荷.下列说法正确的是( )| A. | ac连线上各点场强方向与bd连线上各点的场强方向相同 | |
| B. | 位置b处的电场强度大小为$\frac{\sqrt{2}kq}{{r}^{2}}$ | |
| C. | O点电势低于b点电势 | |
| D. | 将一负试探电荷从b点移到O点,该试探电荷的电势能减小 |
 如图所示,光滑水平面上有A、B两个物块,其质量分别为mA=2.0kg,mB=1.0kg,现用一轻弹簧将A、B两物块连接,并用力缓慢压缩弹簧使A、B两物块靠近,此过程外力做功108J(弹簧仍处于弹性限度范围内),然后同时释放,弹簧开始逐渐变长.试求当弹簧刚好恢复原长时,A和B物块速度vA、vB的大小.
如图所示,光滑水平面上有A、B两个物块,其质量分别为mA=2.0kg,mB=1.0kg,现用一轻弹簧将A、B两物块连接,并用力缓慢压缩弹簧使A、B两物块靠近,此过程外力做功108J(弹簧仍处于弹性限度范围内),然后同时释放,弹簧开始逐渐变长.试求当弹簧刚好恢复原长时,A和B物块速度vA、vB的大小. 如图是用双缝干涉测光的波长的实验装置示意图. 图中①是光源,②是凸透镜,⑤是光屏,可知④是双缝.实验中,使用的双缝的间距为0.02cm,测得双缝与光屏之间的距离为50cm.第1级亮纹中心到第5级亮纹中心距离为0.45cm,则待测单色光的波长是450nm.
如图是用双缝干涉测光的波长的实验装置示意图. 图中①是光源,②是凸透镜,⑤是光屏,可知④是双缝.实验中,使用的双缝的间距为0.02cm,测得双缝与光屏之间的距离为50cm.第1级亮纹中心到第5级亮纹中心距离为0.45cm,则待测单色光的波长是450nm. 如图,在倾角为30°的斜面上,有一个重量为G的物体,当用大小为G的水平恒力F推它时,物体沿斜面匀速向上运动,则物体与斜面间的滑动摩擦系数为多少?
如图,在倾角为30°的斜面上,有一个重量为G的物体,当用大小为G的水平恒力F推它时,物体沿斜面匀速向上运动,则物体与斜面间的滑动摩擦系数为多少?