题目内容
18. 如图所示,质量为M的金属块放在水平地面上,在与水平方向成θ角斜向上、大小为F的拉力作用下,由静止开始向右做加速度为a的匀加速直线运动,重力加速度为g.求:
如图所示,质量为M的金属块放在水平地面上,在与水平方向成θ角斜向上、大小为F的拉力作用下,由静止开始向右做加速度为a的匀加速直线运动,重力加速度为g.求:(1)金属块与地面间的动摩擦因数;
(2)经过时间t撤去拉力F,求撤去拉力后金属块在地面上滑行的时间.
分析 (1)对物体受力分析,根据牛顿第二定律求的摩擦因数;
(2)由运动学公式求的在拉力作用下获得的速度,撤去外力后,根据牛顿第二定律求的加速度,根据运动学公式求的位移
解答 解:(1)分析物体受力如图,由牛顿第二定律得:
Fcosθ-f=Ma①
N+Fsinθ=Mg②
f=μN③
联立①②③解得:$μ=\frac{Fcosθ-Ma}{Mg-Fsinθ}$④
(2)撤去拉力F后,物体受力如图,设物体滑行的时间为t1,
ν=μgt1 ⑤
由匀变速运动公式:v=at⑥
联立④⑤⑥解得:${t_1}=\frac{(Mg-Fsinθ)at}{(Fcosθ-Ma)g}$⑦
答:(1)金属块与地面间的动摩擦因数为$\frac{Fcosθ-Ma}{Mg-Fsinθ}$;
(2)经过时间t撤去拉力F,求撤去拉力后金属块在地面上滑行的时间为$\frac{(Mg-Fsinθ)at}{(Fcosθ-Ma)g}$
点评 本题关键是明确受力分析后,根据牛顿第二定律求解出加速度,然后根据运动学公式确定运动情况

练习册系列答案
相关题目
9.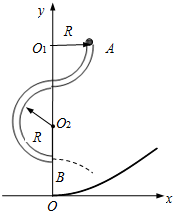 如图所示,在竖直平面内固定着$\frac{3}{4}$光滑圆管轨道.质量为m的小球从轨道顶端A点无初速释放,然后从轨道底端B点水平飞出落在抛物线状坡面上的C点,坡面的抛物线方程为y=$\frac{1}{6R}{x^2}$.已知圆管轨道的半径为R,B点的位置坐标为(0,R),重力加速度为g,忽略空气阻力.则小球( )
如图所示,在竖直平面内固定着$\frac{3}{4}$光滑圆管轨道.质量为m的小球从轨道顶端A点无初速释放,然后从轨道底端B点水平飞出落在抛物线状坡面上的C点,坡面的抛物线方程为y=$\frac{1}{6R}{x^2}$.已知圆管轨道的半径为R,B点的位置坐标为(0,R),重力加速度为g,忽略空气阻力.则小球( )
 如图所示,在竖直平面内固定着$\frac{3}{4}$光滑圆管轨道.质量为m的小球从轨道顶端A点无初速释放,然后从轨道底端B点水平飞出落在抛物线状坡面上的C点,坡面的抛物线方程为y=$\frac{1}{6R}{x^2}$.已知圆管轨道的半径为R,B点的位置坐标为(0,R),重力加速度为g,忽略空气阻力.则小球( )
如图所示,在竖直平面内固定着$\frac{3}{4}$光滑圆管轨道.质量为m的小球从轨道顶端A点无初速释放,然后从轨道底端B点水平飞出落在抛物线状坡面上的C点,坡面的抛物线方程为y=$\frac{1}{6R}{x^2}$.已知圆管轨道的半径为R,B点的位置坐标为(0,R),重力加速度为g,忽略空气阻力.则小球( )| A. | 在B点的速度大小是$2\sqrt{gR}$ | B. | 在B点对轨道的压力大小是7mg | ||
| C. | 在C点的位置坐标是$({\sqrt{2}R,\frac{R}{3}})$ | D. | 在C点的动能是$\frac{10}{3}$mgR |
3. 如图所示为一光电管的工作原理图,光电管能把光信号转变为电信号,当有波长为λ0的光照射光电管的阴极K时,电路中有电流通过灵敏电流计,则有( )
如图所示为一光电管的工作原理图,光电管能把光信号转变为电信号,当有波长为λ0的光照射光电管的阴极K时,电路中有电流通过灵敏电流计,则有( )
 如图所示为一光电管的工作原理图,光电管能把光信号转变为电信号,当有波长为λ0的光照射光电管的阴极K时,电路中有电流通过灵敏电流计,则有( )
如图所示为一光电管的工作原理图,光电管能把光信号转变为电信号,当有波长为λ0的光照射光电管的阴极K时,电路中有电流通过灵敏电流计,则有( )| A. | 用波长为λ1(λ1<λ0)的光照射阴极时,电路中一定没有电流 | |
| B. | 用波长为λ2(λ2<λ0)的光照射阴极时,电路中一定有电流 | |
| C. | 用波长为λ3(λ3>λ0)的光照射阴极时,电路中可能有电流 | |
| D. | 将电源的极性反接后,电路中一定没有电流 |
10. 如图所示,小球质量为m,用长为L的轻质细线悬挂在O点,在O点的正下方处有一钉子P,把细线沿水平方向拉直,无初速度地释放小球,当细线碰到钉子的瞬间,设线没有断裂,则下列说法正确的是( )
如图所示,小球质量为m,用长为L的轻质细线悬挂在O点,在O点的正下方处有一钉子P,把细线沿水平方向拉直,无初速度地释放小球,当细线碰到钉子的瞬间,设线没有断裂,则下列说法正确的是( )
 如图所示,小球质量为m,用长为L的轻质细线悬挂在O点,在O点的正下方处有一钉子P,把细线沿水平方向拉直,无初速度地释放小球,当细线碰到钉子的瞬间,设线没有断裂,则下列说法正确的是( )
如图所示,小球质量为m,用长为L的轻质细线悬挂在O点,在O点的正下方处有一钉子P,把细线沿水平方向拉直,无初速度地释放小球,当细线碰到钉子的瞬间,设线没有断裂,则下列说法正确的是( )| A. | 小球的角速度突然增大 | B. | 小球的瞬时线速度突然增大 | ||
| C. | 小球的向心加速度突然增大 | D. | 小球对悬线的拉力不变 |
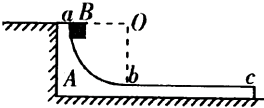 如图所示,A滑块放在光滑的水平面上,B滑块可视为质点,A和B的质量都是1kg,A的左侧面紧靠在光滑竖直墙上,A上表面的ab段是光滑的半径为0.8m的四分之一圆弧,bc段是粗糙的水平丽,ab段与bc段相切于b点.已知bc长度为2m,滑块B从a点由静止开始下滑,取g=10m/s2.
如图所示,A滑块放在光滑的水平面上,B滑块可视为质点,A和B的质量都是1kg,A的左侧面紧靠在光滑竖直墙上,A上表面的ab段是光滑的半径为0.8m的四分之一圆弧,bc段是粗糙的水平丽,ab段与bc段相切于b点.已知bc长度为2m,滑块B从a点由静止开始下滑,取g=10m/s2. 如图所示,一质量为2m、长为L的平板小车静止在光滑水平地面上.一质量为m 的小滑块(可视为质点)静止于小车的左端,现有一质量也为m的子弹以水平向右的速度v0打入小滑块并留在其中,小滑块恰好滑到小车的右端没有掉下.重力加速度为g,求小滑块与小车间动摩擦因数的大小.
如图所示,一质量为2m、长为L的平板小车静止在光滑水平地面上.一质量为m 的小滑块(可视为质点)静止于小车的左端,现有一质量也为m的子弹以水平向右的速度v0打入小滑块并留在其中,小滑块恰好滑到小车的右端没有掉下.重力加速度为g,求小滑块与小车间动摩擦因数的大小. 如图所示,水平传送带保持v=2m/s的速度顺时针转动,现将一小物块轻轻地放在传送带左端上,物块在与传送带相对滑动的过程中做加速度为1m/s2的匀加速运动.已知传送带左、右两端间的距离L=3m,取g=10m/s2,则物块从左端运动到右端所经历的时间为( )
如图所示,水平传送带保持v=2m/s的速度顺时针转动,现将一小物块轻轻地放在传送带左端上,物块在与传送带相对滑动的过程中做加速度为1m/s2的匀加速运动.已知传送带左、右两端间的距离L=3m,取g=10m/s2,则物块从左端运动到右端所经历的时间为( )