题目内容
7. 如图所示,水平传送带保持v=2m/s的速度顺时针转动,现将一小物块轻轻地放在传送带左端上,物块在与传送带相对滑动的过程中做加速度为1m/s2的匀加速运动.已知传送带左、右两端间的距离L=3m,取g=10m/s2,则物块从左端运动到右端所经历的时间为( )
如图所示,水平传送带保持v=2m/s的速度顺时针转动,现将一小物块轻轻地放在传送带左端上,物块在与传送带相对滑动的过程中做加速度为1m/s2的匀加速运动.已知传送带左、右两端间的距离L=3m,取g=10m/s2,则物块从左端运动到右端所经历的时间为( )| A. | 3s | B. | 2.5s | C. | $\sqrt{6}$s | D. | 2s |
分析 然后假设一直加速,根据运动学公式求出加速的位移,再判断物体有没有到达B端,发现没有到达B端,接下来物体做匀速运动直到B端,分匀加速和匀速两个过程,分别求出这两个过程的时间即可
解答 解:设达到与皮带速度v相等时发生的位移为s1,所用时间为t1,则
v2=2as1
代入数据解得:s1=2m<3m
根据速度公式有:v=at1
解得匀加速运动时间为:t1=2s
此时距离B端为:s2=3m-s1=3-2=1m
继续匀速的时间为:t2=$\frac{{s}_{2}}{v}=\frac{1}{2}s=0.5s$
所以有:t=t1+t2=2+0.5=2.5s
故选:B
点评 在传送带上运动的物体,特点是所能达到的最大速度不会超过传送带的速度,关键是判断物体一直加速到达右端还是先加速后匀速

练习册系列答案
相关题目
17.一物体做直线运动,其v-t图象如图所示,从图中可以看出,以下说法正确的是( )
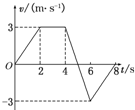

| A. | 只有0~2 s内加速度与速度方向相同 | |
| B. | 5~6 s内物体的加速度为3 m/s2 | |
| C. | 4~6 s 内物体的速度一直在减小 | |
| D. | 0~2 s和5~6 s内加速度的方向与速度方向均相同 |
15. 如图所示,在离地面高为H的地方将质量为m的小球以初速度v0竖直上抛,取抛出位置所在的水平面为参考平面,则小球在最高点和落地处重力势能分别为( )
如图所示,在离地面高为H的地方将质量为m的小球以初速度v0竖直上抛,取抛出位置所在的水平面为参考平面,则小球在最高点和落地处重力势能分别为( )
 如图所示,在离地面高为H的地方将质量为m的小球以初速度v0竖直上抛,取抛出位置所在的水平面为参考平面,则小球在最高点和落地处重力势能分别为( )
如图所示,在离地面高为H的地方将质量为m的小球以初速度v0竖直上抛,取抛出位置所在的水平面为参考平面,则小球在最高点和落地处重力势能分别为( )| A. | mg($\frac{{{v}_{0}}^{2}}{2g}$+H),0 | B. | $\frac{1}{2}$mv02,-mgH | ||
| C. | $\frac{1}{2}$v02m,mgH | D. | $\frac{1}{2}$mv02,mgH+$\frac{1}{2}$mv02 |
2.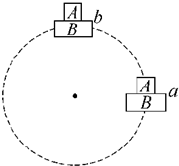 如图所示,水平的木板B托着木块A一起在竖直平面内做匀速圆周运动,从水平位置a沿逆时针方向运动到最高点b的过程中( )
如图所示,水平的木板B托着木块A一起在竖直平面内做匀速圆周运动,从水平位置a沿逆时针方向运动到最高点b的过程中( )
 如图所示,水平的木板B托着木块A一起在竖直平面内做匀速圆周运动,从水平位置a沿逆时针方向运动到最高点b的过程中( )
如图所示,水平的木板B托着木块A一起在竖直平面内做匀速圆周运动,从水平位置a沿逆时针方向运动到最高点b的过程中( )| A. | B对A的支持力先大后小 | B. | B对A的支持力先小后大 | ||
| C. | B对A的摩擦力越来越小 | D. | B对A的摩擦力越来越大 |
12. 有一种有趣的离子运动模型,离子从静止向某个方向运动一段时间后,经过相同时间可回到原处,其物理模型可简化如下.质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用,其大小与时间t的关系如图所示,则( )
有一种有趣的离子运动模型,离子从静止向某个方向运动一段时间后,经过相同时间可回到原处,其物理模型可简化如下.质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用,其大小与时间t的关系如图所示,则( )
 有一种有趣的离子运动模型,离子从静止向某个方向运动一段时间后,经过相同时间可回到原处,其物理模型可简化如下.质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用,其大小与时间t的关系如图所示,则( )
有一种有趣的离子运动模型,离子从静止向某个方向运动一段时间后,经过相同时间可回到原处,其物理模型可简化如下.质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用,其大小与时间t的关系如图所示,则( )| A. | 物体一直沿正方向(原方向)运动 | |
| B. | 2t0时刻的瞬时速度的大小为t0时刻的两倍 | |
| C. | 在t0时刻到2t0时刻这段时间内水平力对物体做负功 | |
| D. | 在t0到2t0这段时间内力做的功是0到t0这段时间的两倍 |
某物理小组的同学设计了一个粗制玩具小车通过凹形桥最低点时的速度的实验。所用器材有:玩具小车、压力式托盘秤、凹形桥模拟器(圆弧部分的半径为R=0.20m)。

完成下列填空:
(1)将凹形桥模拟器静置于托盘秤上,如图(a)所示,托盘秤的示数为1.00kg;
(2)将玩具小车静置于凹形桥模拟器最低点时,托盘秤的示数如图(b)所示,该示数为 kg;
(3)将小车从凹形桥模拟器某一位置释放,小车经过最低点后滑向另一侧,此过程中托盘秤的最大示数为m;多次从同一位置释放小车,记录各次的m值如下表所示:
序号 | 1 | 2 | 3 | 4 | 5 |
m(kg) | 1.80 | 1.75 | 1.85 | 1.75 | 1.90 |
(4)根据以上数据,可求出小车经过凹形桥最低点时对桥的压力为 N;小车通过最低点时的速度大小为 m/s。(重力加速度大小取9.80m/s2,计算结果保留2位有效数字)
 如图所示,质量为M的金属块放在水平地面上,在与水平方向成θ角斜向上、大小为F的拉力作用下,由静止开始向右做加速度为a的匀加速直线运动,重力加速度为g.求:
如图所示,质量为M的金属块放在水平地面上,在与水平方向成θ角斜向上、大小为F的拉力作用下,由静止开始向右做加速度为a的匀加速直线运动,重力加速度为g.求:
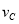 =____________m/s;物体运动的加速度a=___________
=____________m/s;物体运动的加速度a=___________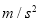 。(计算结果均保留到小数点后两位)
。(计算结果均保留到小数点后两位)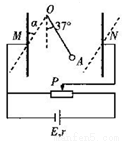
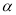 = 30°(用图中虚线表示),并移动滑片位置,欲使绳静止在与竖直方向成30°角的位置,则极板间电压U/是U的多少倍?
= 30°(用图中虚线表示),并移动滑片位置,欲使绳静止在与竖直方向成30°角的位置,则极板间电压U/是U的多少倍?