题目内容
9.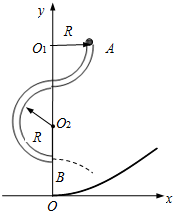 如图所示,在竖直平面内固定着$\frac{3}{4}$光滑圆管轨道.质量为m的小球从轨道顶端A点无初速释放,然后从轨道底端B点水平飞出落在抛物线状坡面上的C点,坡面的抛物线方程为y=$\frac{1}{6R}{x^2}$.已知圆管轨道的半径为R,B点的位置坐标为(0,R),重力加速度为g,忽略空气阻力.则小球( )
如图所示,在竖直平面内固定着$\frac{3}{4}$光滑圆管轨道.质量为m的小球从轨道顶端A点无初速释放,然后从轨道底端B点水平飞出落在抛物线状坡面上的C点,坡面的抛物线方程为y=$\frac{1}{6R}{x^2}$.已知圆管轨道的半径为R,B点的位置坐标为(0,R),重力加速度为g,忽略空气阻力.则小球( )| A. | 在B点的速度大小是$2\sqrt{gR}$ | B. | 在B点对轨道的压力大小是7mg | ||
| C. | 在C点的位置坐标是$({\sqrt{2}R,\frac{R}{3}})$ | D. | 在C点的动能是$\frac{10}{3}$mgR |
分析 据动能定理求出小球在B点时的速度,结合牛顿第二定律求出在B点的支持力,从而得出压力的大小.根据平抛规律可求出小球在坡面上时的竖直分速度,然后求出动能.
解答 解:A、根据动能定理得,$mg•3R=\frac{1}{2}m{{v}_{B}}^{2}$,解得${v}_{B}=\sqrt{6gR}$,故A错误.
B、在B点,根据牛顿第二定律得,$N-mg=m\frac{{{v}_{B}}^{2}}{R}$,解得N=7mg,根据牛顿第三定律知,在B点对轨道的压力为7mg.故B正确.
C、根据平抛规律应有:$x={v}_{B}t=\sqrt{6gR}t$,$R-y=\frac{1}{2}g{t}^{2}$,因为y=$\frac{1}{6R}{x^2}$,解得x=2R,y=$\frac{2}{3}R$,故C错误.
D、落在斜坡上的动能为${E}_{k}=\frac{1}{2}m{{v}_{B}}^{2}+\frac{1}{2}m{{v}_{y}}^{2}$,vy=gt,结合C选项,解得${E}_{k}=\frac{10}{3}mgR$,故D正确.
故选:BD.
点评 应明确:①涉及到圆周运动的动力学问题应根据牛顿第二定律并结合动能定理求解;②涉及到平抛运动问题,应根据平抛规律求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.把电阻是1Ω的一根金属丝,拉长为原来的2倍,导体两端加4v电压,则流过电阻的电流是( )
| A. | 1A | B. | 2A | C. | 3A | D. | 4A |
20.以下关于重力的说法中正确的是( )
| A. | 在落向地球时,物体受的重力大于它静止时受的重力 | |
| B. | 因重力的方向总是竖直向下的,故重力不一定和地面垂直 | |
| C. | 重力就是物体对水平桌面的压力 | |
| D. | 物体的重力随纬度和高度的增加而增大 |
17.一物体做直线运动,其v-t图象如图所示,从图中可以看出,以下说法正确的是( )
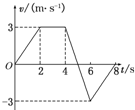

| A. | 只有0~2 s内加速度与速度方向相同 | |
| B. | 5~6 s内物体的加速度为3 m/s2 | |
| C. | 4~6 s 内物体的速度一直在减小 | |
| D. | 0~2 s和5~6 s内加速度的方向与速度方向均相同 |
4.某同学在做“探究小车速度随时间变化规律”的实验时,得到一条点迹清晰的纸带如图1,在纸带上依次选出7个计数点,分别标以O、A、B、C、D、E和F,每相邻的两个计数点间还有四个点未画出,打点计时器所用电源的频率是50Hz.

①如果测得C、D两点间距S4=2.70cm,D、E两点间距S5=2.90cm,若DE之间的时间记为T则据此数据计算在打D点时小车的速度公式为${v}_{D}=\frac{{S}_{4}+{S}_{5}}{2T}$,小车的速度值vD=0.280m/s.(保留三位有效数字)
②该同学分别算出其它速度:vA=0.220m/s,vB=0.241m/s,vC=0.258m/s,vE=0.300m/s,并设计实验数据记录表格填入框中,请在图2坐标系中作出小车运动的v-t图象,设O点为计时起点.

①如果测得C、D两点间距S4=2.70cm,D、E两点间距S5=2.90cm,若DE之间的时间记为T则据此数据计算在打D点时小车的速度公式为${v}_{D}=\frac{{S}_{4}+{S}_{5}}{2T}$,小车的速度值vD=0.280m/s.(保留三位有效数字)
②该同学分别算出其它速度:vA=0.220m/s,vB=0.241m/s,vC=0.258m/s,vE=0.300m/s,并设计实验数据记录表格填入框中,请在图2坐标系中作出小车运动的v-t图象,设O点为计时起点.
| 时间t(s) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| 速度v(m/s) | 0.220 | 0.241 | 0.258 | 0.280 | 0.300 |
14.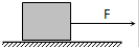 如图所示,一个木块放在水平地面上,在水平恒力F作用下,以速度V匀速运动,下列关于摩擦力的说法正确的是( )
如图所示,一个木块放在水平地面上,在水平恒力F作用下,以速度V匀速运动,下列关于摩擦力的说法正确的是( )
 如图所示,一个木块放在水平地面上,在水平恒力F作用下,以速度V匀速运动,下列关于摩擦力的说法正确的是( )
如图所示,一个木块放在水平地面上,在水平恒力F作用下,以速度V匀速运动,下列关于摩擦力的说法正确的是( )| A. | 地面受到的静摩擦力的大小等于F | |
| B. | 木块受到的滑动摩擦力的大小等于F | |
| C. | 若木块以2V速度匀速运动时,木块受到的摩擦力的大小等于2F | |
| D. | 若用2F的力作用在木块上,木块受到摩擦力的大小为2F |
1.一物体静置在斜面上,关于它所受各力的相互关系,下列说法正确的是( )
| A. | 它受的重力与弹力相等 | |
| B. | 它受的弹力是因为物体发生形变产生的 | |
| C. | 所受的弹力与摩擦力的产生条件都要直接接触和发生形变,所以它们的方向一致的 | |
| D. | 它所受的弹力垂直于斜面向上 |
 如图所示,质量为M的金属块放在水平地面上,在与水平方向成θ角斜向上、大小为F的拉力作用下,由静止开始向右做加速度为a的匀加速直线运动,重力加速度为g.求:
如图所示,质量为M的金属块放在水平地面上,在与水平方向成θ角斜向上、大小为F的拉力作用下,由静止开始向右做加速度为a的匀加速直线运动,重力加速度为g.求:
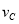 =____________m/s;物体运动的加速度a=___________
=____________m/s;物体运动的加速度a=___________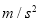 。(计算结果均保留到小数点后两位)
。(计算结果均保留到小数点后两位)