题目内容
6.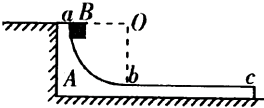 如图所示,A滑块放在光滑的水平面上,B滑块可视为质点,A和B的质量都是1kg,A的左侧面紧靠在光滑竖直墙上,A上表面的ab段是光滑的半径为0.8m的四分之一圆弧,bc段是粗糙的水平丽,ab段与bc段相切于b点.已知bc长度为2m,滑块B从a点由静止开始下滑,取g=10m/s2.
如图所示,A滑块放在光滑的水平面上,B滑块可视为质点,A和B的质量都是1kg,A的左侧面紧靠在光滑竖直墙上,A上表面的ab段是光滑的半径为0.8m的四分之一圆弧,bc段是粗糙的水平丽,ab段与bc段相切于b点.已知bc长度为2m,滑块B从a点由静止开始下滑,取g=10m/s2.(1)求滑块B滑到b点时对A的压力大小;
(2)若滑块B恰好能滑到A的最右端,此时B与bc段的动摩擦因数μ为多少;
(3)μ值满足0.1≤μ≤0.5,试讨论因μ值的不同,滑块B在滑块A上相对A运动过程中两者因摩擦而产生的热量(计算结果可含有μ).
分析 滑块滑到B点由机械能守恒定律求得速度大小,由牛顿第二定律求解滑块B滑到b点时对A的压力大小;根据动量守恒定律求出共同的速度,由能量守恒定律求解.
解答 解:(1)设滑块B下滑到b点时的速度v0,此时A对滑块的弹力为N, 由机械能守恒有:${m_B}gR=\frac{1}{2}{m_B}v_0^2$…①
由机械能守恒有:${m_B}gR=\frac{1}{2}{m_B}v_0^2$…①
由牛顿第二定律有:$N-{m_B}g={m_B}\frac{v_0^2}{R}$…②
滑块B滑到b点对对A的压力大小为:N'=N…③
联立①②③式并代入数据解得:N'=30N…④
(2)B滑到b点后,A、B组成的系统动量守恒,B恰好滑到A最右端时,刚好能够共速为v,由动量守恒定律得:mv0=2mv…⑤
由能量守恒得:${μ_1}mgl=\frac{1}{2}mv_0^2-\frac{1}{2}(2m){v^2}$…⑥
联立①⑤⑥式并代入数据解得:μ1=0.2…⑦
(3)①当满足0.1≤μ<0.2时,A和B不能共速,B将从A的右端滑落,A和B因摩擦而产生的热量为:Q1=μmgl=20μJ…⑧
②当满足0.2≤μ≤0.5时,A和B能共速且速度为v,A和B因摩擦而产生的热量为:${Q_2}=\frac{1}{2}mv_0^2-\frac{1}{2}(2m){v^2}$…⑨
联立①⑤⑨式并代数据解得:Q2=4J…⑩
答:(1)滑块B滑到b点时对A的压力大小为30N;
(2)若滑块B恰好能滑到A的最右端,此时B与bc段的动摩擦因数μ为0.2
(3)0.1≤μ<0.2时,因摩擦而产生的热量为20μJ
0.2≤μ≤0.5时,因摩擦而产生的热量为4J
点评 本题首先要分析物理过程,确定研究对象,其次要把握解题的规律,采用机械能守恒、动量守恒和能量守恒结合研究,难度适中

练习册系列答案
相关题目
16.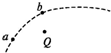 如图所示,点电荷Q固定,虚线是电荷量为q的微粒的运动轨迹,微粒的重力不计,a、b是轨迹上的两个点,b离Q较近,下列判断不正确的是( )
如图所示,点电荷Q固定,虚线是电荷量为q的微粒的运动轨迹,微粒的重力不计,a、b是轨迹上的两个点,b离Q较近,下列判断不正确的是( )
 如图所示,点电荷Q固定,虚线是电荷量为q的微粒的运动轨迹,微粒的重力不计,a、b是轨迹上的两个点,b离Q较近,下列判断不正确的是( )
如图所示,点电荷Q固定,虚线是电荷量为q的微粒的运动轨迹,微粒的重力不计,a、b是轨迹上的两个点,b离Q较近,下列判断不正确的是( )| A. | Q与q带的电荷一定是一正一负 | |
| B. | 微粒通过a时的速率比通过b时的速率大 | |
| C. | 不管Q带什么性质的电荷,a点的电场强度一定比b点的小 | |
| D. | 微粒通过a、b两点时,加速度方向都是指向Q |
17.一物体做直线运动,其v-t图象如图所示,从图中可以看出,以下说法正确的是( )
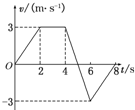

| A. | 只有0~2 s内加速度与速度方向相同 | |
| B. | 5~6 s内物体的加速度为3 m/s2 | |
| C. | 4~6 s 内物体的速度一直在减小 | |
| D. | 0~2 s和5~6 s内加速度的方向与速度方向均相同 |
14.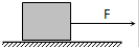 如图所示,一个木块放在水平地面上,在水平恒力F作用下,以速度V匀速运动,下列关于摩擦力的说法正确的是( )
如图所示,一个木块放在水平地面上,在水平恒力F作用下,以速度V匀速运动,下列关于摩擦力的说法正确的是( )
 如图所示,一个木块放在水平地面上,在水平恒力F作用下,以速度V匀速运动,下列关于摩擦力的说法正确的是( )
如图所示,一个木块放在水平地面上,在水平恒力F作用下,以速度V匀速运动,下列关于摩擦力的说法正确的是( )| A. | 地面受到的静摩擦力的大小等于F | |
| B. | 木块受到的滑动摩擦力的大小等于F | |
| C. | 若木块以2V速度匀速运动时,木块受到的摩擦力的大小等于2F | |
| D. | 若用2F的力作用在木块上,木块受到摩擦力的大小为2F |
1.一物体静置在斜面上,关于它所受各力的相互关系,下列说法正确的是( )
| A. | 它受的重力与弹力相等 | |
| B. | 它受的弹力是因为物体发生形变产生的 | |
| C. | 所受的弹力与摩擦力的产生条件都要直接接触和发生形变,所以它们的方向一致的 | |
| D. | 它所受的弹力垂直于斜面向上 |
11.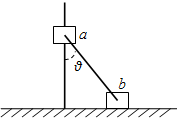 如图,小滑块a、b通过铰链用刚性轻杆连接,a套在固定竖直杆上,b放在水平地面上,a竖直下滑,当ab间的轻杆与竖直方向夹角为θ时,a的速度为v,则此时b沿水平地面向右运动的速度大小为( )
如图,小滑块a、b通过铰链用刚性轻杆连接,a套在固定竖直杆上,b放在水平地面上,a竖直下滑,当ab间的轻杆与竖直方向夹角为θ时,a的速度为v,则此时b沿水平地面向右运动的速度大小为( )
 如图,小滑块a、b通过铰链用刚性轻杆连接,a套在固定竖直杆上,b放在水平地面上,a竖直下滑,当ab间的轻杆与竖直方向夹角为θ时,a的速度为v,则此时b沿水平地面向右运动的速度大小为( )
如图,小滑块a、b通过铰链用刚性轻杆连接,a套在固定竖直杆上,b放在水平地面上,a竖直下滑,当ab间的轻杆与竖直方向夹角为θ时,a的速度为v,则此时b沿水平地面向右运动的速度大小为( )| A. | $\frac{v}{tanθ}$ | |
| B. | vtanθ | |
| C. | vcosθ | |
| D. | 因为不知道是否有摩擦,所以b的速度不能确定 |
15. 如图所示,在离地面高为H的地方将质量为m的小球以初速度v0竖直上抛,取抛出位置所在的水平面为参考平面,则小球在最高点和落地处重力势能分别为( )
如图所示,在离地面高为H的地方将质量为m的小球以初速度v0竖直上抛,取抛出位置所在的水平面为参考平面,则小球在最高点和落地处重力势能分别为( )
 如图所示,在离地面高为H的地方将质量为m的小球以初速度v0竖直上抛,取抛出位置所在的水平面为参考平面,则小球在最高点和落地处重力势能分别为( )
如图所示,在离地面高为H的地方将质量为m的小球以初速度v0竖直上抛,取抛出位置所在的水平面为参考平面,则小球在最高点和落地处重力势能分别为( )| A. | mg($\frac{{{v}_{0}}^{2}}{2g}$+H),0 | B. | $\frac{1}{2}$mv02,-mgH | ||
| C. | $\frac{1}{2}$v02m,mgH | D. | $\frac{1}{2}$mv02,mgH+$\frac{1}{2}$mv02 |
 如图所示,质量为M的金属块放在水平地面上,在与水平方向成θ角斜向上、大小为F的拉力作用下,由静止开始向右做加速度为a的匀加速直线运动,重力加速度为g.求:
如图所示,质量为M的金属块放在水平地面上,在与水平方向成θ角斜向上、大小为F的拉力作用下,由静止开始向右做加速度为a的匀加速直线运动,重力加速度为g.求: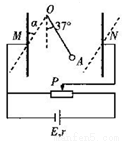
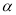 = 30°(用图中虚线表示),并移动滑片位置,欲使绳静止在与竖直方向成30°角的位置,则极板间电压U/是U的多少倍?
= 30°(用图中虚线表示),并移动滑片位置,欲使绳静止在与竖直方向成30°角的位置,则极板间电压U/是U的多少倍?