题目内容
【题目】构建理想化模型，是处理物理问题常见的方法。
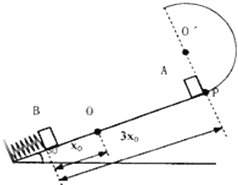
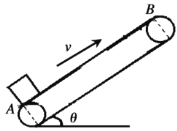
（1）在研究平行板电容器的相关问题时，我们是从研究理想化模型——无限大带电平面开始的。真空中无限大带电平面的电场是匀强电场，电场强度为E0=
，其中k是静电力常量，σ为电荷分布在平面上的面密度，单位为C/m2。如图1所示，无限大平面带正电，电场指向两侧。若带负电则电场指向中央（图中未画出）。在实际问题中，当两块相同的带等量异种电荷的较大金属板相距很近时，其中间区域，可以看作是两个无限大带电平面所产生的匀强电场叠加；如果再忽略边缘效应，平行板电容器两板间的电场就可以看作是匀强电场，如图2所示。已知平行板电容器所带电量为Q，极板面积为S，板间距为d，求：
a. 两极板间电场强度的大小E；
b. 请根据电容的定义式，求出在真空中，该平行板电容器的电容C；
c. 求解图2中左极板所受电场力的大小F。
（提示：因为带电左极板的存在已经影响到带电右极板单独存在时空间场强的分布，所以不能使用a问中计算出的场强，而是应该将电场强度“还原”到原来右极板单独存在时，在左极板所在位置产生的电场强度。）
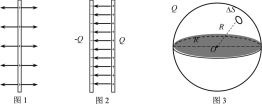
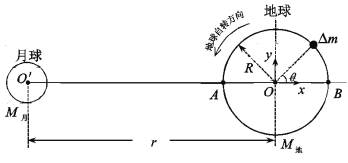
（2）根据以上思路，请求解真空中均匀带电球面（理想化模型，没有厚度）上某微小面元所受电场力。如图3所示，已知球面半径为R，所带电量为Q，该微小面元的面积为S，带电球面在空间的电场强度分布为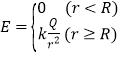
，其中r为空间某点到球心O的距离。
（提示：“无限大”是相对的，在实际研究中，只要被研究点距离带电面足够近，就可认为该带电面为无限大带电平面）
【答案】（1）a.
b. 
c. 
（2）
,方向背向圆心向外，表现为扩张力.
【解析】
（1）a.由电场的叠加可知，平行板电容器内部的电场是正负极板上的电荷产生的电场的矢量和，由电场的叠加原理可得：
b.电容器极板间的电势差为：
，在由电容器的电容的定义式可得：
c.由题意可知右极板产生的匀强电场，电场强度为E0=
，所以左极板受力：
（2）取距离微小面元无限近的两点M和N，分别位于带电球体的内表面和外表面；由题意可知：①微小面元在MN两点产生的场强大小为：
，方向分别指向球心和背向球心；
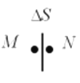
②由带电球面在空间的场强分布可知，M点处场强为零，因此除去小面元S以外的带电球面在M点产生的场强与小面元在M点产生的场强大小相等，方向相反，即场强大小为
，方向背向球心（由N点计算的场强也为
）
因此，除去面元S以外的带电球面在面元S处所产生的场强，由此得打该面元所受的电场力
,方向背向圆心向外，表现为扩张力.
