题目内容
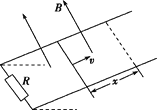
【题目】两条平行导轨倾斜地固定在绝缘地面上，导轨间距为d，在导轨的底端连接一阻值为R的定值电阻，在空间加一垂直导轨平面向上的匀强磁场，将一质量为m、阻值为R、长度为d的金属杆垂直地放在导轨上，给金属杆一沿斜面向上的大小为v的初速度，当其沿导轨向上运动的位移大小为x时，速度减为零，已知导轨的倾角为α、金属杆与导轨之间的动摩擦因数为μ、重力加速度为g．则金属杆从出发到到达最高点的过程中，下列说法正确的是( )
A. 金属杆所受安培力的最大值为
B. 金属杆克服安培力做的功为
C. 定值电阻产生的热量为
D. 金属杆减少的机械能为
【答案】BD
【解析】
A、金属杆开始运动时速度最大，产生的感应电动势和感应电流最大，所受的安培力最大，由
、
、
得最大安培力为
，故选项A错误；
B、根据能量守恒定律可知，上滑过程中电流做功产生的热量为：
，由功能关系可知金属杆克服安培力做的功为
，故选项B正确；
C、由于整个电路所产生的热量为
，则定值电阻产生的热量为
，故选项C错误；
D、上滑的过程中金属杆的动能减少
，重力势能增加
，所以金属杆损失的机械能为 
，故选项D正确；
故选选项BD。
练习册系列答案
相关题目
