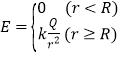题目内容
【题目】如图所示，在倾角为30°的光滑斜面上放置一质量为m的物块B，B的下端连接一轻质弹簧，弹簧下端与挡板相连接，B平衡时，弹簧的压缩量为x0，O点为弹簧的原长位置．在斜面顶端另有一质量为m的物块A，距物块B为3x0，现让A从静止开始沿斜面下滑，A与B相碰后立即一起沿斜面向下运动，但不粘连，它们到达最低点后又一道向上运动，并恰好回到O点（A、B均视为质点）．试求：
（1）A、B相碰后瞬间的共同速度的大小；
（2）A、B相碰前弹簧具有的弹性势能；
（3）若在斜面顶端再连接一光滑的半径R＝x0的半圆轨道PQ，圆轨道与斜面相切于最高点P，现让物块A以初速度v从P点沿斜面下滑，与B碰后返回到P点还具有向上的速度，试问：v为多大时物块A恰能通过圆弧轨道的最高点？
【答案】
【解析】
试题（1）A与B球碰撞前后，A球的速度分别是v1和v2，因A球滑下过程中，机械能守恒，有：
mg（3x0）sin30°=
mv12
解得：
…①
又因A与B球碰撞过程中，动量守恒，有：mv1=2mv2…②
联立①②得：
（2）碰后，A、B和弹簧组成的系统在运动过程中，机械能守恒．
则有：EP+2mv22＝0+2mgx0sin30°
解得：EP＝2mgx0sin30°2mv22=mgx0
mgx0＝
mgx0…③
（3）设物块在最高点C的速度是vC，
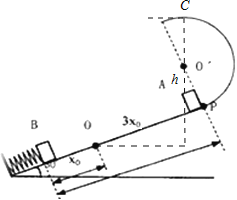
物块A恰能通过圆弧轨道的最高点C点时，重力提供向心力，得：
所以：
④
C点相对于O点的高度：
h=2x0sin30°+R+Rcos30°=
x0…⑤
物块从O到C的过程中机械能守恒，得：mvo2＝mgh+mvc2…⑥
联立④⑤⑥得：
…⑦
设A与B碰撞后共同的速度为vB，碰撞前A的速度为vA，滑块从P到B的过程中机械能守恒，得：mv2+mg（3x0sin30°）＝mvA2…⑧
A与B碰撞的过程中动量守恒．得：mvA=2mvB…⑨
A与B碰撞结束后从Bspan>到O的过程中机械能守恒，得：2mvB2+EP＝2mvo2+2mgx0sin30°…⑩
由于A与B不粘连，到达O点时，滑块B开始受到弹簧的拉力，A与B分离．
联立⑦⑧⑨⑩解得：
同步练习强化拓展系列答案
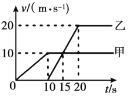
【题目】将两个金属电极锌片和铜片插入一个水果中就可以做成一个水果电池，通过前期查阅相关资料，得知其电动势约为1.3~2.0V，内阻约为400~800Ω。某兴趣小组为了精确测量水果电池的电动势和内阻利用滑动变阻器R(0-3kΩ)，毫安表
满偏电流3mA，电阻约10Ω)电压表
(量程0-2.0V，电阻约1000Ω)，开关导线等设计了如图甲、乙两种实验电路。
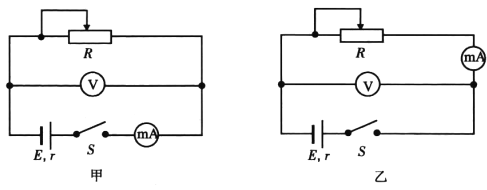
(1)为了使结果更加精确，本实验应该选择_________图的电路(填“甲”或“乙”).
(2)按照所选电路进行实验，得到多组电压表示数U和电流表示数I，并记录在下表内.
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
电压 | 1.28 | 1.08 | 0.89 | 0.75 | 0.64 | 0.42 | 0.40 | 0.18 |
电流 | 0.47 | 0.84 | 1.23 | 1.48 | 1.69 | 1.87 | 2.13 | 2.52 |
请根据测量数据在答题卡的坐标纸中描出第5、6组数据，并作出U-I图线________.
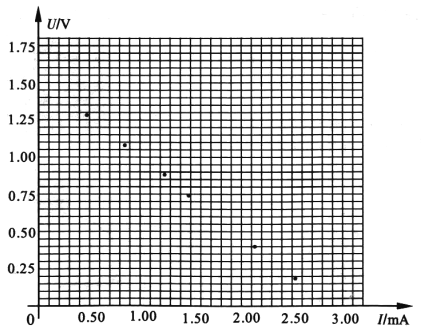
(3)根据U-I图像，可知此水果电池的电动势为________V，内阻为______Ω(结果保留三位有效数字).
