题目内容
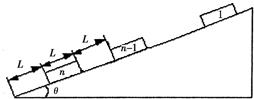 如图所示,n个相同的货箱停放在倾角为θ的斜面上,每个货箱长为L、质量为m,相邻两个货箱间距为L,最下端的货箱到斜面底端的距离也为L.现给第一个货箱一初速度使之沿斜面下滑,在每次发生碰撞后,发生碰撞的货箱都粘合在一起向下运动,最后第n个货箱恰好停在斜面的底端.设每个货箱与斜面间的动摩擦因数均为μ.求:
如图所示,n个相同的货箱停放在倾角为θ的斜面上,每个货箱长为L、质量为m,相邻两个货箱间距为L,最下端的货箱到斜面底端的距离也为L.现给第一个货箱一初速度使之沿斜面下滑,在每次发生碰撞后,发生碰撞的货箱都粘合在一起向下运动,最后第n个货箱恰好停在斜面的底端.设每个货箱与斜面间的动摩擦因数均为μ.求:(1)第n个货箱开始运动时的加速度大小.
(2)第n个货箱开始运动时的速度大小.
(3)整个过程中由于货箱与斜面间的摩擦而损失的机械能.
分析:本题(1)的关键是对整个货箱应用牛顿第二定律即可求解;(2)题的关键是明确第n个货箱做匀减速运动的位移为L,然后运用运动速度关系即可求解;(3)题的关键是求出每个货箱克服摩擦力做的功,然后累加,再根据数学知识即可求解.
解答: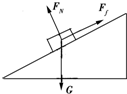 解:(1)第n个货箱开始运动时,有n个货箱粘合在一起向下运动,其受力如图所示,因为第n个货箱恰好停在斜面的底端,所以,货箱作的是减速运动.由牛顿第二定律有:
解:(1)第n个货箱开始运动时,有n个货箱粘合在一起向下运动,其受力如图所示,因为第n个货箱恰好停在斜面的底端,所以,货箱作的是减速运动.由牛顿第二定律有:
μnmgcosθ-nmgsinθ=nma
解得:a=μgcosθ-gsinθ
故第n个货箱开始运动时的加速度大小为a=μgcosθ-gsinθ
(2)设第n个货箱开始运动时的速度为v,由匀变速直线运动规律可得:
0-
=-2aL
解得:v=
故第n个货箱开始运动时的速度大小为v=
.
(3)整个过程中由于货箱与斜面间的摩擦而损失的机械能为:
△E=μmgcosθ?nL+μmgcosθ?(n-1)L+μmgcosθ?(n-2)L+…+μmgcosθ?L
=
μmgcosθ?L
故整个过程中由于货箱与斜面间的摩擦而损失的机械能为△E=
μmgLcosθ
 解:(1)第n个货箱开始运动时,有n个货箱粘合在一起向下运动,其受力如图所示,因为第n个货箱恰好停在斜面的底端,所以,货箱作的是减速运动.由牛顿第二定律有:
解:(1)第n个货箱开始运动时,有n个货箱粘合在一起向下运动,其受力如图所示,因为第n个货箱恰好停在斜面的底端,所以,货箱作的是减速运动.由牛顿第二定律有:μnmgcosθ-nmgsinθ=nma
解得:a=μgcosθ-gsinθ
故第n个货箱开始运动时的加速度大小为a=μgcosθ-gsinθ
(2)设第n个货箱开始运动时的速度为v,由匀变速直线运动规律可得:
0-
| v | 2 |
解得:v=
| 2gL(μcosθ-sinθ) |
故第n个货箱开始运动时的速度大小为v=
| 2gL(μcosθ-sinθ) |
(3)整个过程中由于货箱与斜面间的摩擦而损失的机械能为:
△E=μmgcosθ?nL+μmgcosθ?(n-1)L+μmgcosθ?(n-2)L+…+μmgcosθ?L
=
| n(n+1) |
| 2 |
故整个过程中由于货箱与斜面间的摩擦而损失的机械能为△E=
| n(n+1) |
| 2 |
点评:正确选取研究对象进行受力分析,然后选取相应的物理规律即可求解.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
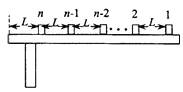
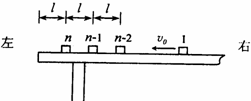 如图所示,n个相同的木块(可视为质点),每块的质量都是m,从右向左沿同一直线排列在水平桌面上,相邻木块间的距离均为l,第n个木块到桌边的距离也是l,木块与桌面间的动摩擦因数为μ.开始时,第1个木块以初速度υ0向左滑行,其余所有木块都静止,在每次碰撞后,发生碰撞的木块都粘在一起运动.最后第n个木块刚好滑到桌边而没有掉下.
如图所示,n个相同的木块(可视为质点),每块的质量都是m,从右向左沿同一直线排列在水平桌面上,相邻木块间的距离均为l,第n个木块到桌边的距离也是l,木块与桌面间的动摩擦因数为μ.开始时,第1个木块以初速度υ0向左滑行,其余所有木块都静止,在每次碰撞后,发生碰撞的木块都粘在一起运动.最后第n个木块刚好滑到桌边而没有掉下. 如图所示,n个相同的木块(可视为质点),每块的质量都是m,从右向左沿同一直线排列在水平桌面上,相邻木块间的距离均为l,第n个木块到桌边的距离也是l,木块与桌面间的动摩擦因数为??.开始时,第1个木块以初速度v0向左滑行,其余所有木块都静止,在每次碰撞后,发生碰撞的木块都粘在一起运动.最后第n个木块刚好滑到桌边而没有掉下.
如图所示,n个相同的木块(可视为质点),每块的质量都是m,从右向左沿同一直线排列在水平桌面上,相邻木块间的距离均为l,第n个木块到桌边的距离也是l,木块与桌面间的动摩擦因数为??.开始时,第1个木块以初速度v0向左滑行,其余所有木块都静止,在每次碰撞后,发生碰撞的木块都粘在一起运动.最后第n个木块刚好滑到桌边而没有掉下.