题目内容
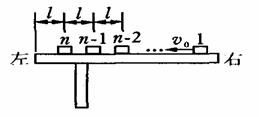
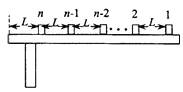
 如图所示,n个相同的木块(可视为质点),每块的质量都是m,从右向左沿同一直线排列在水平桌面上,相邻木块间的距离均为l,第n个木块到桌边的距离也是l,木块与桌面间的动摩擦因数为??.开始时,第1个木块以初速度v0向左滑行,其余所有木块都静止,在每次碰撞后,发生碰撞的木块都粘在一起运动.最后第n个木块刚好滑到桌边而没有掉下.
如图所示,n个相同的木块(可视为质点),每块的质量都是m,从右向左沿同一直线排列在水平桌面上,相邻木块间的距离均为l,第n个木块到桌边的距离也是l,木块与桌面间的动摩擦因数为??.开始时,第1个木块以初速度v0向左滑行,其余所有木块都静止,在每次碰撞后,发生碰撞的木块都粘在一起运动.最后第n个木块刚好滑到桌边而没有掉下.
(1)求在整个过程中因碰撞而损失的总动能.
(2)求第i次(i≤n-1)碰撞中损失的动能与碰撞前动能之比.
(3)若n=4,l=0.10m,v0=3.0m/s,重力加速度g=10m/s2,求??的数值.
(1)![]() ;(2)
;(2)![]() ;(3)0.15
;(3)0.15
解析:
(1)整个过程中系统克服摩擦力做的总功为
Wf=??mgl(1+2+3+…+n)=![]()
![]()
整个过程中因碰撞而损失的总动能为
![]()
(2)设第i次(i≤n-1)碰撞前瞬间,前i个木块粘合在一起的速度为vi,动能为
![]()
与第i+1个(i≤n-1)木块碰撞粘合在一起后瞬间的速度为vi',由动量守恒定律得
![]() ,则
,则
![]()
第i次(i≤n-1)碰撞中损失的动能为
![]()
则第i次(i≤n-1)碰撞中损失的动能与碰撞前动能之比为
![]() (i≤n-1)
(i≤n-1)
(3)n=4时,共发生了i=3次碰撞.
第1次碰前瞬间的速度为![]() ,碰撞中动量守恒
,碰撞中动量守恒![]()
第1次碰后瞬间的速度为![]()
第2次碰前瞬间的速度为![]()
碰撞中动量守恒![]()
第2次碰后瞬间的速度为![]()
第3次碰前瞬间的速度为![]()
碰撞中动量守恒![]()
第3次碰后瞬间的速度为![]()
最后滑行到桌边,速度恰好为零,则![]()
即![]()
整理后得![]() ,代入数据解得
,代入数据解得![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
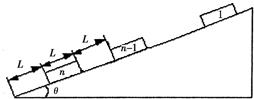 如图所示,n个相同的货箱停放在倾角为θ的斜面上,每个货箱长为L、质量为m,相邻两个货箱间距为L,最下端的货箱到斜面底端的距离也为L.现给第一个货箱一初速度使之沿斜面下滑,在每次发生碰撞后,发生碰撞的货箱都粘合在一起向下运动,最后第n个货箱恰好停在斜面的底端.设每个货箱与斜面间的动摩擦因数均为μ.求:
如图所示,n个相同的货箱停放在倾角为θ的斜面上,每个货箱长为L、质量为m,相邻两个货箱间距为L,最下端的货箱到斜面底端的距离也为L.现给第一个货箱一初速度使之沿斜面下滑,在每次发生碰撞后,发生碰撞的货箱都粘合在一起向下运动,最后第n个货箱恰好停在斜面的底端.设每个货箱与斜面间的动摩擦因数均为μ.求: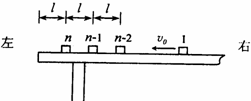 如图所示,n个相同的木块(可视为质点),每块的质量都是m,从右向左沿同一直线排列在水平桌面上,相邻木块间的距离均为l,第n个木块到桌边的距离也是l,木块与桌面间的动摩擦因数为μ.开始时,第1个木块以初速度υ0向左滑行,其余所有木块都静止,在每次碰撞后,发生碰撞的木块都粘在一起运动.最后第n个木块刚好滑到桌边而没有掉下.
如图所示,n个相同的木块(可视为质点),每块的质量都是m,从右向左沿同一直线排列在水平桌面上,相邻木块间的距离均为l,第n个木块到桌边的距离也是l,木块与桌面间的动摩擦因数为μ.开始时,第1个木块以初速度υ0向左滑行,其余所有木块都静止,在每次碰撞后,发生碰撞的木块都粘在一起运动.最后第n个木块刚好滑到桌边而没有掉下.