��Ŀ����
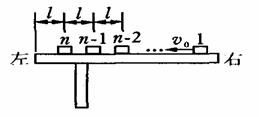
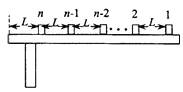
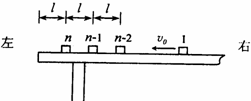 ��ͼ��ʾ��n����ͬ��ľ�飨����Ϊ�ʵ㣩��ÿ�����������m������������ͬһֱ��������ˮƽ�����ϣ�����ľ���ľ����Ϊl����n��ľ�鵽���ߵľ���Ҳ��l��ľ���������Ķ�Ħ������Ϊ�̣���ʼʱ����1��ľ���Գ��ٶȦ�0�����У���������ľ�鶼��ֹ����ÿ����ײ������ײ��ľ�鶼ճ��һ���˶�������n��ľ��պû������߶�û�е��£�
��ͼ��ʾ��n����ͬ��ľ�飨����Ϊ�ʵ㣩��ÿ�����������m������������ͬһֱ��������ˮƽ�����ϣ�����ľ���ľ����Ϊl����n��ľ�鵽���ߵľ���Ҳ��l��ľ���������Ķ�Ħ������Ϊ�̣���ʼʱ����1��ľ���Գ��ٶȦ�0�����У���������ľ�鶼��ֹ����ÿ����ײ������ײ��ľ�鶼ճ��һ���˶�������n��ľ��պû������߶�û�е��£���1��������������������ײ����ʧ���ܶ��ܣ�
��2�����i�Σ�i��nһ1����ײ����ʧ�Ķ�������ײǰ����֮�ȣ�
��3����n=4��l=0.10m����0=3.0m/s���������ٶ�g=10m/s2����̵���ֵ��
��������1������������������ײ��Ħ����ʧ���ܶ��ܵ��ڳ����ܡ�Ek=
m
������˷�Ħ�����������õ���Ħ������ʧ�Ķ��ܣ������������ײ����ʧ���ܶ��ܣ�
��2�����ݶ����غ㶨�������i�Σ�i��nһ1����ײǰ���ٶȹ�ϵ�����������ײ����ʧ�Ķ�������ײǰ����֮�ȣ�
��3���ֱ���ø�����ײǰ��Ķ��ܣ��õ���3����ײ��Ķ��ܣ�������⣺��n=4��ľ��պû������߶�û�е��£����ù��ܹ�ϵ��̣�
| 1 |
| 2 |
| v | 2 0 |
��2�����ݶ����غ㶨�������i�Σ�i��nһ1����ײǰ���ٶȹ�ϵ�����������ײ����ʧ�Ķ�������ײǰ����֮�ȣ�
��3���ֱ���ø�����ײǰ��Ķ��ܣ��õ���3����ײ��Ķ��ܣ�������⣺��n=4��ľ��պû������߶�û�е��£����ù��ܹ�ϵ��̣�
����⣺��1����������ľ��˷�Ħ��������
W=��mgl+��mg?2l+��+��mg?nl=
��
���ݹ��ܹ�ϵ������������������ײ����ʧ���ܶ���Ϊ
��Ek=Ek0-W ��
�á�Ek=
m
-
��
��2�����i�Σ�i��nһ1����ײǰľ����ٶ�Ϊ��i����ײ���ٶ�Ϊ��i�䣬��
��i+1��m��i��=im��i ��
��ײ����ʧ�Ķ��ܡ�Eʱ����ײǰ����Eki֮��Ϊ
=
��i��n-1����
���
=
��i��n-1����
��3��������Ek0=
m
��1����ײǰ
=EK0-��mgl ��
��1����ײ�� EK1��=EK1-��EK1=EK1-
EK1=
EK0-
��mgl ��
��2����ײǰ EK2=EK1��=�̣�2mg��l=
EK0-
��mgl
��2����ײ�� EK2��=EK2-��EK2=
EK0-
��mgl
��3����ײǰ EK3=EK3��-�̣�3mg��l=
EK0-
��mgl
��3����ײ�� EK3��=EK3-��EK3=
EK0-
��mgl
��������
EK0-
��mgl=�̣�4mg��l ��
�������ݣ��������� ��=0.15 ��
��
��1������������������ײ����ʧ���ܶ���Ϊ
m
-
��
��2����i�Σ�i��nһ1����ײ����ʧ�Ķ�������ײǰ����֮��Ϊ1����i+1����
��3����n=4��l=0.10m����0=3.0m/s���������ٶ�g=10m/s2���̵���ֵ��0.15��
W=��mgl+��mg?2l+��+��mg?nl=
| n(n+1)��mgl |
| 2 |
���ݹ��ܹ�ϵ������������������ײ����ʧ���ܶ���Ϊ
��Ek=Ek0-W ��
�á�Ek=
| 1 |
| 2 |
| v | 2 0 |
| n(n+1)��mgl |
| 2 |
��2�����i�Σ�i��nһ1����ײǰľ����ٶ�Ϊ��i����ײ���ٶ�Ϊ��i�䣬��
��i+1��m��i��=im��i ��
��ײ����ʧ�Ķ��ܡ�Eʱ����ײǰ����Eki֮��Ϊ
| ��EKi |
| EKi |
| ||||||||
|
���
| ��EKi |
| EKi |
| 1 |
| i+1 |
��3��������Ek0=
| 1 |
| 2 |
| v | 2 0 |
��1����ײǰ
| E | K1 |
��1����ײ�� EK1��=EK1-��EK1=EK1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��2����ײǰ EK2=EK1��=�̣�2mg��l=
| 1 |
| 2 |
| 1 |
| 2 |
��2����ײ�� EK2��=EK2-��EK2=
| 1 |
| 3 |
| 5 |
| 3 |
��3����ײǰ EK3=EK3��-�̣�3mg��l=
| 1 |
| 3 |
| 14 |
| 3 |
��3����ײ�� EK3��=EK3-��EK3=
| 1 |
| 4 |
| 7 |
| 2 |
��������
| 1 |
| 4 |
| 7 |
| 2 |
�������ݣ��������� ��=0.15 ��
��
��1������������������ײ����ʧ���ܶ���Ϊ
| 1 |
| 2 |
| v | 2 0 |
| n(n+1)��mgl |
| 2 |
��2����i�Σ�i��nһ1����ײ����ʧ�Ķ�������ײǰ����֮��Ϊ1����i+1����
��3����n=4��l=0.10m����0=3.0m/s���������ٶ�g=10m/s2���̵���ֵ��0.15��
�����������Ƕ����غ��빦�ܹ�ϵ��ϵ����ͣ����ù��ɷ�������ɴ���ײ�Ĺ��̣��ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
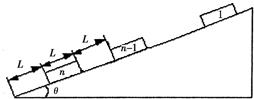 ��ͼ��ʾ��n����ͬ�Ļ���ͣ�������Ϊ�ȵ�б���ϣ�ÿ�����䳤ΪL������Ϊm����������������ΪL�����¶˵Ļ��䵽б��˵ľ���ҲΪL���ָ���һ������һ���ٶ�ʹ֮��б���»�����ÿ�η�����ײ������ײ�Ļ��䶼ճ����һ�������˶�������n������ǡ��ͣ��б��ĵˣ���ÿ��������б���Ķ�Ħ��������Ϊ�̣���
��ͼ��ʾ��n����ͬ�Ļ���ͣ�������Ϊ�ȵ�б���ϣ�ÿ�����䳤ΪL������Ϊm����������������ΪL�����¶˵Ļ��䵽б��˵ľ���ҲΪL���ָ���һ������һ���ٶ�ʹ֮��б���»�����ÿ�η�����ײ������ײ�Ļ��䶼ճ����һ�������˶�������n������ǡ��ͣ��б��ĵˣ���ÿ��������б���Ķ�Ħ��������Ϊ�̣��� ��ͼ��ʾ��n����ͬ��ľ��������Ϊ�ʵ㣩��ÿ�����������m������������ͬһֱ��������ˮƽ�����ϣ�����ľ���ľ����Ϊl����n��ľ�鵽���ߵľ���Ҳ��l��ľ���������Ķ�Ħ������Ϊ??����ʼʱ����1��ľ���Գ��ٶ�v0�����У���������ľ�鶼��ֹ����ÿ����ײ������ײ��ľ�鶼ճ��һ���˶�������n��ľ��պû������߶�û�е��£�
��ͼ��ʾ��n����ͬ��ľ��������Ϊ�ʵ㣩��ÿ�����������m������������ͬһֱ��������ˮƽ�����ϣ�����ľ���ľ����Ϊl����n��ľ�鵽���ߵľ���Ҳ��l��ľ���������Ķ�Ħ������Ϊ??����ʼʱ����1��ľ���Գ��ٶ�v0�����У���������ľ�鶼��ֹ����ÿ����ײ������ײ��ľ�鶼ճ��һ���˶�������n��ľ��պû������߶�û�е��£�