��Ŀ����
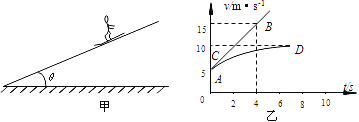
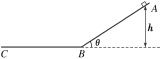
����Ŀ��һ���Ϊ����![]() ���߶�Ϊh��1m��б��AB��ˮƽ��BC��B��ƽ��������һ����m��2kg�Ļ����б�涥��A���ɾ�ֹ��ʼ�»�������B�������ͣ��C�㡣��֪������Ӵ����Ķ�Ħ��������Ϊ����
���߶�Ϊh��1m��б��AB��ˮƽ��BC��B��ƽ��������һ����m��2kg�Ļ����б�涥��A���ɾ�ֹ��ʼ�»�������B�������ͣ��C�㡣��֪������Ӵ����Ķ�Ħ��������Ϊ����![]() �����ƻ�����B���������ʧ��gȡ10m/s2��������˵���������(����)
�����ƻ�����B���������ʧ��gȡ10m/s2��������˵���������(����)
A.���鵽��B�����ٶ�Ϊ![]() m/s
m/s
B.�����A����B���õ�ʱ��Ϊ![]() s
s
C.BC���Ϊ![]() m
m
D.�����B��C�Ĺ����У��˷�Ħ���������Ĺ�Ϊ10J
���𰸡�B
��������
A����A��B�����ݶ��ܶ�����
![]()
�������ݽ��
vB��![]() m/s
m/s
��A��ȷ��
B����ţ�ٵڶ�������
![]()
����
![]()
�������ݽ��
![]()
��B����
C����B��C�����ݶ��ܶ����ã�
����mgLBC��0��![]() mvB2
mvB2
�������ݵ�
LBC��![]() m��C��ȷ��
m��C��ȷ��
D���ɶ��ܶ�����
Wf��0��![]() mv2����10J
mv2����10J
��D��ȷ��
��ѡB��

��ϰ��ϵ�д�
 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
�����Ŀ