题目内容
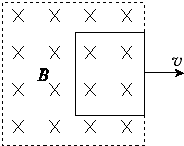
【题目】如图所示,ef,gh为水平放置的足够长的平行光滑导轨,导轨间距为L=1m,导轨左端连接一个R=2Ω的电阻,将一根质量为0.2kg的金属棒cd垂直地放置导轨上,且与导轨接触良好,导轨与金属棒的电阻均不计,整个装置放在磁感应强度为B=2T的匀强磁场中,磁场方向垂直于导轨平面向下.现对金属棒施加一水平向右的拉力F,使棒从静止开始向右运动.试解答以下问题.
(1)若施加的水平外力恒为F=8N,则金属棒达到的稳定速度v1是多少?
(2)若施加的水平外力的功率恒为P=18W,则金属棒达到的稳定速度v2是多少?
(3)若施加的水平外力的功率恒为P=18W,则金属棒从开始运动到速度v3=2m/s的过程中电阻R产生的热量为8.6J,则该过程所需的时间是多少?
【答案】
(1)解:当棒的速度为v时,则有 E=BLv,I= ![]() ,F=BIL,则安培力F=
,F=BIL,则安培力F= ![]() .
.
若施加的水平外力恒为F=8N,金属棒达到稳定时做匀速运动,由平衡条件得:
F= ![]() ,得:
,得: ![]() =
= ![]() m/s=4m/s
m/s=4m/s
答:若施加的水平外力恒为F=8N,金属棒达到的稳定速度v1是4m/s.
(2)解:若施加的水平外力的功率恒为P=18W,金属棒达到稳定时水平外力大小为F= ![]()
由平衡条件得:
![]() =
= ![]() ,得:
,得: ![]() =
= ![]() m/s=3m/s
m/s=3m/s
答:若施加的水平外力的功率恒为P=18W,金属棒达到的稳定速度v2是3m/s.
(3)解:若施加的水平外力的功率恒为P=18W,金属棒从开始运动到速度v3=2m/s的过程中,水平外力做功为Pt,根据能量守恒定律得:
Pt= ![]() +Q
+Q
代入解得:t=0.5s
答:该过程所需的时间是0.5s.
【解析】(1)当施加水平恒力时,棒先做变加速运动,后做匀速运动,达到稳定状态,恒力与安培力平衡,由平衡条件求出速度v1.(2)若施加的水平外力的功率恒定时,稳定时棒也做匀速运动,此时的外力大小为 ![]() ,由平衡条件求出速度v2.(3)金属棒从开始运动到速度v3=2m/s的过程中,水平外力做功为Pt,外界提供的能量转化为棒的动能和电路中的电能,根据能量守恒定律列式求解该过程所需的时间.
,由平衡条件求出速度v2.(3)金属棒从开始运动到速度v3=2m/s的过程中,水平外力做功为Pt,外界提供的能量转化为棒的动能和电路中的电能,根据能量守恒定律列式求解该过程所需的时间.
【考点精析】根据题目的已知条件,利用电磁感应与电路和电磁感应与力学的相关知识可以得到问题的答案,需要掌握用法拉第电磁感应定律和楞次定律确定感应电动势的大小和方向;画等效电路;运用全电路欧姆定律,串并联电路性质,电功率等公式联立求解;用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向;求回路中电流强度;分析研究导体受力情况(包含安培力,用左手定则确定其方向);列动力学方程或平衡方程求解.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案