题目内容
11.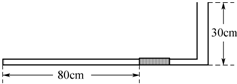 如图所示,L形一端开口的玻璃管在竖直平面内,管是由粗细不同的两部分组成的,竖直部分粗管的横截面积是水平部分细管横截面积的2倍,管的封闭端水平放置,水平段管长为100cm,竖直段管长为30cm,在水平管内有一段长为12cm的水银封闭着一段长为80cm的空气柱.已知气柱的温度为27℃,大气压强为75cmHg,现对气体缓慢加热,求:当温度上升到119℃时,封闭端空气柱的长度.
如图所示,L形一端开口的玻璃管在竖直平面内,管是由粗细不同的两部分组成的,竖直部分粗管的横截面积是水平部分细管横截面积的2倍,管的封闭端水平放置,水平段管长为100cm,竖直段管长为30cm,在水平管内有一段长为12cm的水银封闭着一段长为80cm的空气柱.已知气柱的温度为27℃,大气压强为75cmHg,现对气体缓慢加热,求:当温度上升到119℃时,封闭端空气柱的长度.
分析 首先假设水银柱还全部在水平管内,此过程被封闭的气体压强不变,计算当温度变为119℃时,气体的长度,与水平管的长度相比较,判断是否合理.再假设进入竖直管的水银高度为xcm,分析此时的状态参量,列式进行求解.
解答 解:设水银柱将要进入竖直管内所需温度为t1,由气体状态方程:
$\frac{{P}_{1}{V}_{1}}{{T}_{1}}=\frac{{P}_{2}{V}_{2}}{{T}_{2}}$,
P1=P2
即$\frac{80}{273+27}=\frac{88}{273+{t}_{1}}$,
解得:t1=57C°
设水银柱刚好全部到竖直管内所需温度为t2,由气体状态方程:
$\frac{{P}_{1}{V}_{1}}{{T}_{1}}=\frac{{P}_{3}{V}_{3}}{{T}_{3}}$
$\frac{75×80}{273+27}=\frac{(75+6)×100}{273+{t}_{2}}$
解得:
t2=132C°
可见119C°时水平管内还有水银,设竖直管内水银柱高为x,
则$\frac{75×80}{300}$=$\frac{(75+x)×(100-12+2x)}{392}$
解得:x=5 cm
所以空气柱长为98 cm;
答:当温度上升到119℃时,封闭端空气柱的长度为98cm.
点评 判断水银柱是否能进入竖直管是解决此问题的关键之一,要学会应用假设法来判断此问题;当有水银进入竖直管后,判断被封闭气体的压强也是解决此问题的关键,注意找出水平管内和竖直管内水银柱的长度的关系.是一道好题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
1.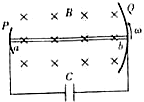 如图所示,在空间存在着竖直向下的匀强磁场,磁感应强度为B.一水平放置的长度为L的金属杆ab与圆弧形金属导轨P、Q紧密接触,P、Q之间接有电容为C的电容器.若ab杆绕a点以角速度ω沿逆时针方向匀速转动,则下列说法正确的是( )
如图所示,在空间存在着竖直向下的匀强磁场,磁感应强度为B.一水平放置的长度为L的金属杆ab与圆弧形金属导轨P、Q紧密接触,P、Q之间接有电容为C的电容器.若ab杆绕a点以角速度ω沿逆时针方向匀速转动,则下列说法正确的是( )
 如图所示,在空间存在着竖直向下的匀强磁场,磁感应强度为B.一水平放置的长度为L的金属杆ab与圆弧形金属导轨P、Q紧密接触,P、Q之间接有电容为C的电容器.若ab杆绕a点以角速度ω沿逆时针方向匀速转动,则下列说法正确的是( )
如图所示,在空间存在着竖直向下的匀强磁场,磁感应强度为B.一水平放置的长度为L的金属杆ab与圆弧形金属导轨P、Q紧密接触,P、Q之间接有电容为C的电容器.若ab杆绕a点以角速度ω沿逆时针方向匀速转动,则下列说法正确的是( )| A. | 电容器与a相连的极板带正电 | B. | 电容器与b相连的极板带正电 | ||
| C. | 电容器的带电量是$\frac{CB{ω}^{2}L}{2}$ | D. | 电容器的带电量是$\frac{CBω{L}^{2}}{2}$ |
2.分子动理论的基本观点:物体是由大量分子组成的、分子的热运动、分子间的相互作用力.下列说法中正确的是( )
| A. | 布朗运动是液体分子的运动,它说明分子永不停息地做无规则运动 | |
| B. | 扩散现象表明,分子在永不停息地运动 | |
| C. | 当分子间距离增大时,分子间引力增大,分子间斥力减小 | |
| D. | 当分子间距等于r0时,分子间的引力和斥力都为零 |
19.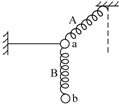 如图所示,小球a的质量为小球b质量的一半,分别与轻弹簧A、B和轻绳相连接并处于平衡状态.轻弹簧A与竖直方向夹角为60°,轻弹簧A、B伸长量刚好相同,则下列说法中正确的是( )
如图所示,小球a的质量为小球b质量的一半,分别与轻弹簧A、B和轻绳相连接并处于平衡状态.轻弹簧A与竖直方向夹角为60°,轻弹簧A、B伸长量刚好相同,则下列说法中正确的是( )
 如图所示,小球a的质量为小球b质量的一半,分别与轻弹簧A、B和轻绳相连接并处于平衡状态.轻弹簧A与竖直方向夹角为60°,轻弹簧A、B伸长量刚好相同,则下列说法中正确的是( )
如图所示,小球a的质量为小球b质量的一半,分别与轻弹簧A、B和轻绳相连接并处于平衡状态.轻弹簧A与竖直方向夹角为60°,轻弹簧A、B伸长量刚好相同,则下列说法中正确的是( )| A. | 轻弹簧A、B的劲度系数之比为3:1 | |
| B. | 轻弹簧A、B的劲度系数之比为2:1 | |
| C. | 轻绳上拉力与轻弹簧A上拉力大小之比为2:1 | |
| D. | 轻绳上拉力与轻弹簧B上拉力大小之比为1:1 |
6.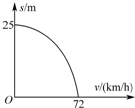 某司机在检测汽车性能过程中,得到汽车减速过程中的位移s与速度v的关系曲线如图所示,并得出位移s与速度v的函数关系式为s=m-nv2,其中m、n为常数.重力加速度的大小g取10m/s2.则以下判断正确的是( )
某司机在检测汽车性能过程中,得到汽车减速过程中的位移s与速度v的关系曲线如图所示,并得出位移s与速度v的函数关系式为s=m-nv2,其中m、n为常数.重力加速度的大小g取10m/s2.则以下判断正确的是( )
 某司机在检测汽车性能过程中,得到汽车减速过程中的位移s与速度v的关系曲线如图所示,并得出位移s与速度v的函数关系式为s=m-nv2,其中m、n为常数.重力加速度的大小g取10m/s2.则以下判断正确的是( )
某司机在检测汽车性能过程中,得到汽车减速过程中的位移s与速度v的关系曲线如图所示,并得出位移s与速度v的函数关系式为s=m-nv2,其中m、n为常数.重力加速度的大小g取10m/s2.则以下判断正确的是( )| A. | 汽车在此过程中做匀变速直线运动 | |
| B. | 汽车的末速度为20m/s | |
| C. | 由题中所给已知条件可确定m、n的大小 | |
| D. | 汽车对司机作用力的大小与司机重力大小的比值为$\frac{4}{5}$ |
3.下列叙述中,正确的是( )
| A. | 熵增加原理说明一切自然过程总是向着分子热运动的无序性减小的方向进行 | |
| B. | 一定量100℃的水变成100℃的水蒸气,其分子之间的势能增加 | |
| C. | 气体如果失去容器的约束就会散开,这是因为气体分子之间存在斥力的缘故 | |
| D. | 一定质量的理想气体从外界吸收热量,其内能可能不变 | |
| E. | 水可以浸润玻璃,但是不能浸润石蜡,这个现象表明一种液体是否浸润某种固体与这两种物质的性质都有关系 |