题目内容
19.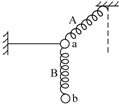 如图所示,小球a的质量为小球b质量的一半,分别与轻弹簧A、B和轻绳相连接并处于平衡状态.轻弹簧A与竖直方向夹角为60°,轻弹簧A、B伸长量刚好相同,则下列说法中正确的是( )
如图所示,小球a的质量为小球b质量的一半,分别与轻弹簧A、B和轻绳相连接并处于平衡状态.轻弹簧A与竖直方向夹角为60°,轻弹簧A、B伸长量刚好相同,则下列说法中正确的是( )| A. | 轻弹簧A、B的劲度系数之比为3:1 | |
| B. | 轻弹簧A、B的劲度系数之比为2:1 | |
| C. | 轻绳上拉力与轻弹簧A上拉力大小之比为2:1 | |
| D. | 轻绳上拉力与轻弹簧B上拉力大小之比为1:1 |
分析 先对球b分析,根据平衡条件求解弹簧B的弹力;再对球a、b整体受力分析,根据平衡条件求解细线的拉力和弹簧A的弹力,最后结合胡克定律分析弹簧A、B的劲度系数之比为.
解答 解:AB、对小球b受力分析,受重力和拉力,受力平衡,弹簧B的弹力:
FB=mbg;
对小球a、b整体受力分析,如图所示: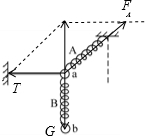
根据平衡条件,弹簧A的拉力:
FA=2(ma+mb)g,
mb=2ma,
又由胡克定律F=kx,弹簧A、B伸长量刚好相同,轻弹簧A、B的劲度系数之比:
$\frac{{k}_{A}}{{k}_{B}}=\frac{{F}_{A}}{{F}_{B}}=\frac{3}{1}$
故A正确,B错误;
CD、根据平衡条件,有:
FB=mbg
FA=2(ma+mb)g
T=(ma+mb)gtan60°=$\sqrt{3}({m}_{a}+{m}_{b})g$
故轻绳上拉力与轻弹簧A上拉力大小之比为:
$\frac{T}{{F}_{A}}=\frac{\sqrt{3}}{2}$
轻绳上拉力与轻弹簧B上拉力大小之比为:
$\frac{T}{{F}_{B}}=\frac{3\sqrt{3}}{2}$
故C错误,D错误;
故选:A
点评 本题关键是采用整体法和隔离法灵活选择研究对象,然后根据平衡条件并结合合成法和胡克定律列式求解,不难.

练习册系列答案
相关题目
9.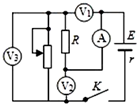 如图所示的电路中,定值电阻R的阻值大于电源内阻r的阻值,将滑动变阻器滑片向下滑动,理想电压表V1、V2、V3示数变化量的绝对值分别为△U1、△U2、△U3,理想电流表A示数变化量的绝对值为△I,则( )
如图所示的电路中,定值电阻R的阻值大于电源内阻r的阻值,将滑动变阻器滑片向下滑动,理想电压表V1、V2、V3示数变化量的绝对值分别为△U1、△U2、△U3,理想电流表A示数变化量的绝对值为△I,则( )
 如图所示的电路中,定值电阻R的阻值大于电源内阻r的阻值,将滑动变阻器滑片向下滑动,理想电压表V1、V2、V3示数变化量的绝对值分别为△U1、△U2、△U3,理想电流表A示数变化量的绝对值为△I,则( )
如图所示的电路中,定值电阻R的阻值大于电源内阻r的阻值,将滑动变阻器滑片向下滑动,理想电压表V1、V2、V3示数变化量的绝对值分别为△U1、△U2、△U3,理想电流表A示数变化量的绝对值为△I,则( )| A. | A的示数增大 | B. | △U1小于△U2 | ||
| C. | △U3与△I的比值等于r | D. | 电阻R消耗的功率一定增大 |
10.如图所示,人站在自动扶梯上随扶梯匀速上升,下列说法中正确的是( )
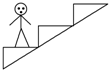

| A. | 人所受的合力方向与自动扶梯运动方向相同 | |
| B. | 人在水平方向将受到向右的摩擦力的作用 | |
| C. | 人只在竖直方向受力作用,且合力为零 | |
| D. | 人在竖直方向所受力的合力不为零 |
4.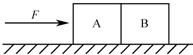 如图所示,物块A、B质量相等,在恒力F作用下,在水平面上做匀加速直线运动.若物块与水平面间接触面光滑,物块A的加速度大小为a1,物块A、B间的相互作用力大小为N1;若物块与水平面间接触面粗糙,且物块A、B与水平面间的动摩擦因数相同,物块B的加速度大小为a2,物块A、B间的相互作用力大小为N2,则以下判断正确的是( )
如图所示,物块A、B质量相等,在恒力F作用下,在水平面上做匀加速直线运动.若物块与水平面间接触面光滑,物块A的加速度大小为a1,物块A、B间的相互作用力大小为N1;若物块与水平面间接触面粗糙,且物块A、B与水平面间的动摩擦因数相同,物块B的加速度大小为a2,物块A、B间的相互作用力大小为N2,则以下判断正确的是( )
 如图所示,物块A、B质量相等,在恒力F作用下,在水平面上做匀加速直线运动.若物块与水平面间接触面光滑,物块A的加速度大小为a1,物块A、B间的相互作用力大小为N1;若物块与水平面间接触面粗糙,且物块A、B与水平面间的动摩擦因数相同,物块B的加速度大小为a2,物块A、B间的相互作用力大小为N2,则以下判断正确的是( )
如图所示,物块A、B质量相等,在恒力F作用下,在水平面上做匀加速直线运动.若物块与水平面间接触面光滑,物块A的加速度大小为a1,物块A、B间的相互作用力大小为N1;若物块与水平面间接触面粗糙,且物块A、B与水平面间的动摩擦因数相同,物块B的加速度大小为a2,物块A、B间的相互作用力大小为N2,则以下判断正确的是( )| A. | a1=a2 | B. | a1>a2 | C. | N1=N2 | D. | N1<N2 |
9.已知氘核的平均结合能是1.09MeV,氚核的平均结合能是2.78MeV,氦核的平均结合能是7.03MeV.在某次核反应中,1个氘核和1个氚核结合生成1个氦核并放出17.6MeV的能量,下列说法正确的是( )
| A. | 这是一个裂变反应 | |
| B. | 核反应方程式为${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n | |
| C. | 目前核电站都采用上述核反应发电 | |
| D. | 该核反应不会有质量亏损 |
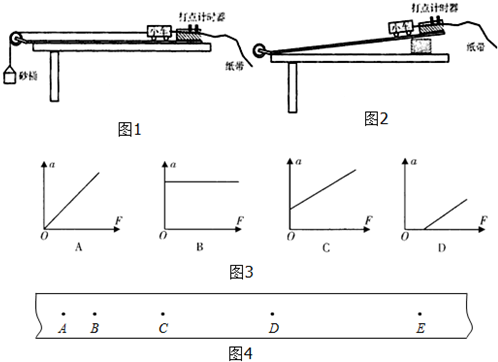
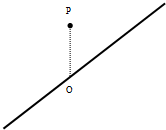 一足够大的倾角为45°的斜面上有一点O,O点正上方h=0.4m处有一点P.在P点以水平速度v0=1m/s抛出一个小球,随着抛出方向的不同,小球将落到斜面上的不同位置.不计空气阻力,重力加速度g取10m/s2.试求小球落到斜面上的位置距离O点的最大值和最小值.
一足够大的倾角为45°的斜面上有一点O,O点正上方h=0.4m处有一点P.在P点以水平速度v0=1m/s抛出一个小球,随着抛出方向的不同,小球将落到斜面上的不同位置.不计空气阻力,重力加速度g取10m/s2.试求小球落到斜面上的位置距离O点的最大值和最小值.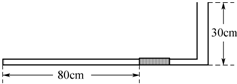 如图所示,L形一端开口的玻璃管在竖直平面内,管是由粗细不同的两部分组成的,竖直部分粗管的横截面积是水平部分细管横截面积的2倍,管的封闭端水平放置,水平段管长为100cm,竖直段管长为30cm,在水平管内有一段长为12cm的水银封闭着一段长为80cm的空气柱.已知气柱的温度为27℃,大气压强为75cmHg,现对气体缓慢加热,求:当温度上升到119℃时,封闭端空气柱的长度.
如图所示,L形一端开口的玻璃管在竖直平面内,管是由粗细不同的两部分组成的,竖直部分粗管的横截面积是水平部分细管横截面积的2倍,管的封闭端水平放置,水平段管长为100cm,竖直段管长为30cm,在水平管内有一段长为12cm的水银封闭着一段长为80cm的空气柱.已知气柱的温度为27℃,大气压强为75cmHg,现对气体缓慢加热,求:当温度上升到119℃时,封闭端空气柱的长度.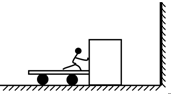 如图所示,小车与木箱紧挨着静止放在光滑的水平冰面上(冰面足够大),现有一男孩站在小车上用力向右迅速推出木箱.推出木箱后人和车的速度大小为4m/s,木箱与竖直墙壁碰撞反弹后恰好不能追上小车.已知人和车的总质量为100kg,木箱的质量为25kg.求:
如图所示,小车与木箱紧挨着静止放在光滑的水平冰面上(冰面足够大),现有一男孩站在小车上用力向右迅速推出木箱.推出木箱后人和车的速度大小为4m/s,木箱与竖直墙壁碰撞反弹后恰好不能追上小车.已知人和车的总质量为100kg,木箱的质量为25kg.求: