题目内容
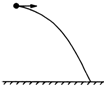
如图所示，在倾角为θ的光滑斜面A点处，以初速度v0与斜面成α角斜抛出一小球．小球下落时将与斜面做弹性碰撞．若小球返跳回出发点A，则α、θ满足的条件是（ ）
| A．cotαcotθ=k | B．cotαtanθ=k | C．sinαcosθ=k | D．cosαsinθ=k |
将运动过程分解成垂直斜面和平行于斜面的两个运动．到达斜面的顶端时，
沿斜面方向的初速度：vx0=v0cosα，末速度：vx=0．沿斜面方向的加速度：ax=-gsinθ，所以运动的时间：t=
=
…①
垂直于斜面的方向：vy0=v0sinα，加速度：ay=gcosθ，所以运动的时间：t=
=
…②
联立①②解得：tanα=2tanθ．故选项B正确．
故选：B
沿斜面方向的初速度：vx0=v0cosα，末速度：vx=0．沿斜面方向的加速度：ax=-gsinθ，所以运动的时间：t=
| △vx |
| gsinθ |
| v0cosα |
| gsinθ |
垂直于斜面的方向：vy0=v0sinα，加速度：ay=gcosθ，所以运动的时间：t=
| 2vy0 |
| ay |
| 2v0sinα |
| gcosθ |
联立①②解得：tanα=2tanθ．故选项B正确．
故选：B
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
