题目内容
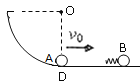
【题目】如图所示，光滑的
圆弧轨道竖直放置，底端与光滑的水平轨道相接，质量为
的小球B静止在光滑水平轨道上，其左侧连接了一轻质弹簧，质量为
的小球A从D点以速度
向右运动，试求：
（1）小球A撞击轻质弹簧的过程中，弹簧弹性势能的最大值；
（2）要使小球A与小球B能发生二次碰撞， 
与
应满足什么关系．
【答案】（1）
,（2）
.
【解析】试题分析：小球A撞击轻质弹簧的过程中，当两球速度相等时，弹簧的弹性势能最大，由动量守恒定律与机械能守恒定律可以求出弹簧的最大弹性势能；两球分开后，若A球的速度大于B球的速度时，两球可以第二次相碰，由动量守恒定律与机械能守恒定律可以求出两球发生第二次相碰的条件。
（1）小球A撞击轻质弹簧的过程中，当A、B两球速度相同时，弹簧的弹性势能最大，设共同速度为v，取向右为正方向，根据动量守恒定律有： 
根据机械能守恒定律有： 
联立解得弹簧弹性势能的最大值为： 
（2）设A、B与弹簧分离后的速度分别为v1和v2
根据动量守恒定律有： 
根据机械能守恒定律有： 
联立解得： 
， 
要使A、B两球能发生二次碰撞，必须满足|v1|＞v2
则有： 
解得： 
，（m1+m2＜0不符合事实，舍去）
练习册系列答案
相关题目
