题目内容
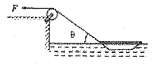
【题目】如图所示,长为l=2.5m的光滑斜面AB,其倾角为θ=300,水平地面粗糙,动摩擦系数μ=0.5,质量为m=2kg的物块从斜面顶端A点静上滑下,它在B点无能量损失, g取10 m/s2.求:
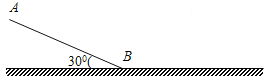
(1)物块到底端B点的速度v;
(2)物块在水平地面上运动的距离;
(3)物块在水平地面上运动的时间;
(4)摩擦力在水平地面上的功率.
【答案】(1)5m/s(2)x=2.5m(3)1s(4)-25W
【解析】试题分析:对物块受力分析,应用牛顿第二定律求出加速,再根据速度位移公式即可求出速度度和距离;在由速度时间公式求出时间,根据功率表达式求出摩擦力的功率。
(1)物块在斜面上受重力和支持力,由牛顿第二定律得:mgsinθ=ma
解得:a=gsinθ=5m/s2
由速度位移公式得: ![]()
代入数据解得: v=5 m/s
(2)在水平面上的加速度为:-μmg =ma1
解得:a1= -μg=-5 m/s2
由速度位移公式: ![]()
解得:x=2.5m
(3)根据速度时间公式: v=v0+at
带入数据解得: t=1s
(4)摩擦力在水平地面上的功率为: ![]() 25W
25W

【题目】在“探究加速度与力、质量的关系”实验中,某同学组装了如图甲所示的装置.
(1)关于平衡摩擦力的操作过程,下列说法中正确的是

A.应将长木板的左端适当垫高 |
B.应将砝码盘通过细绳与小车相连 |
C.应将纸带穿过打点计时器并与小车相连 |
D.应使小车在长木板上保持静止 |
(2)平衡摩擦力后,保持砝码盘和砝码的总质量不变,改变小车的质量M,进行实验,算出加速度a,记录在如下的表格中.第3次实验的纸带如图乙所示,从比较清晰的点起,每五个点取一个计数点,分别标上0、l、2、3、4……,测得1与 2两点间距离x1=30.0mm,2与3两点间的距离x2=32.5mm,实验中所用交流电源的频率为50 Hz,由此算出加速度大小为 m/s2.

(3)为了能直观地反映出小车的加速度a与质量M的关系,应作 (选填“a-M”或“a-![]() ”)图象.
”)图象.