题目内容
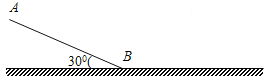
【题目】如图所示，半径R=1.25m的
光滑圆弧轨道AB竖直固定，其末端B切线水平，并与水平传送带相连，已知小滑块的质量为m=0.5kg，滑块与传送带间的动摩擦因数μ=0.1，传送带BC长度为s=1.5m，a、b两轮半径r=0.4m，当传送带静止时，用F=4N的水平拉力将滑块从C端由静止开始向左拉力．（g取10m/s2）
（1）若滑块到达B端时撤去拉力F，则滑块沿弧形槽上升的最大高度为多少？
（2）问题（1）中的滑块，从高处沿弧形槽再滑回B端时，轨道对滑块的支持力多大？
（3）若a、b两轮以角速度ω=15rad/s顺时针转动，滑块在水平拉力F作用下从C点从静止开始移动一段水平距离后撤去，滑块到达光滑曲面某一高度而下滑时，为使滑块能在b轮最高点C离开传送带飞出，则拉力F作用的最短距离需多大？
【答案】（1）滑块沿弧形槽上升的最大高度为1.05m；
（2）轨道对滑块的支持力为13.4N；
（3）拉力F作用的最短距离需0.25m．
【解析】解：（1）根据动能定理有：WF+WG+Wf=Ek一Ek0=0
即：Fs﹣mgh﹣μmgs=0，
代入数值解得：h=1.05 m．
（2）从高处滑回B点过程中，根据机械能守恒定律有：mgh=
，
在B点有：NB﹣mg=m
，
解以上两式得：NB=mg+2mg
代入数据解得：NB=13.4 N
（3）根据题意，滑块要从b轮最高点C离开传送带飞出，则滑块运动至C点的速度最小为：
mg=m
，
即：vC=
=
=2 m/s．
由于传送带的速度v带=rω=6 m/s，滑块在B点的速度0＜vB≤
，要使滑块从C点以2 m/s飞出，可分析出滑块在传送带上从B到C做匀加速运动．（1分）
根据牛顿第二定律，可得加速度为：a=
=
=μg=1 m/s2，为了使滑块运动到C点时速度大于2 m/s，
则B点的速度最小为：
=2as，
代入数据可得：vBmin=1 m/s．
设拉力F作用的最短距离为x，则根据动能定理有：
Fx﹣fs=
m
﹣0，
代入数据可以求得：x=0.25 m．
答：（1）滑块沿弧形槽上升的最大高度为1.05m；
（2）轨道对滑块的支持力为13.4N；
（3）拉力F作用的最短距离需0.25m．
