题目内容
【题目】如图所示,位于竖直平面内的轨道,由一段斜的直轨道AB和光滑半圆形轨道BC平滑连接而成,AB的倾角为30°,半圆形轨道的半径.R=0.1m,直径BC竖直.质量m=1kg的小物块从斜轨道上距半圆形轨道底部高为h处由静止开始下滑,经B点滑上半圆形轨道.己知物块与斜轨道间的动摩擦因数为 ![]() ,g取g=10m/s2 .
,g取g=10m/s2 . 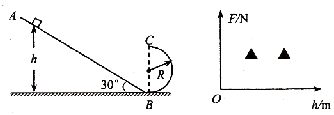
(1)若h=1m,求物块运动到圆轨道最低点B时对轨道的压力;
(2)若物块能到达圆轨道的最高点C,求h的最小值;
(3)试求物块经最高点C时对轨道压力F随高度h的变化关系,并在图示坐标系中作出F﹣h图象.
【答案】
(1)解:设物块运动圆轨道最低点B时速度大小为v,所受的支持力为N.
根据动能定理有:mgh﹣μmgcos30° ![]() =
= ![]() ﹣0
﹣0
在B点,根据牛顿第二定律有:N﹣mg=m ![]()
代入数据,解得 N=110N
根据牛顿第三定律知,物块对轨道的压力大小为110N,方向竖直向下.
(2)解:设物块恰好能到达圆轨道的最高点C,此时对应的高度为hmin,C点的速度为v0.
根据动能定理有:mghmin﹣μmgcos30° ![]() ﹣2mgR=﹣0
﹣2mgR=﹣0
经最高点C时,根据向心力公式有:mg=m ![]()
代入数据,解得 hmin=0.5m
(3)解:设物块到达圆轨道最高点时的速度为v,轨道对物块的弹力大小为FN.
根据动能定理有:mgh﹣μmgcos30° ![]() ﹣2mgR=
﹣2mgR= ![]() ﹣0
﹣0
经最高点C,根据向心力公式有:FN+mg=m ![]()
解得 FN=100h﹣50(N)(h≥0.5m)
则压力 F=FN=100h﹣50(N)(h≥0.5m),作出F﹣h图象如图.
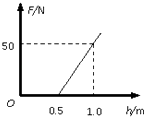
【解析】(1)对于物块在斜面下滑的过程,由机动能定理即可求得物体通过B点时的速度,物块经过B点时,由轨道的支持力和重力的合力充当向心力,由牛顿运动定律求物块对轨道的压力;(2)物块恰好通过圆轨道的最高点C时由重力提供向心力,此时h最小.由牛顿第二定律求出C点的最小速度,再由动能定理求解h的最小值.(3)根据动能定理和向心力公式结合得到F与h的表达式,再画出F﹣h图象.
【考点精析】解答此题的关键在于理解动能定理的综合应用的相关知识,掌握应用动能定理只考虑初、末状态,没有守恒条件的限制,也不受力的性质和物理过程的变化的影响.所以,凡涉及力和位移,而不涉及力的作用时间的动力学问题,都可以用动能定理分析和解答,而且一般都比用牛顿运动定律和机械能守恒定律简捷.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】在“探究小车速度随时间变化的规律”的实验中,打点计时器使用的交流电的频率为50Hz,记录小车运动的纸带如图所示,在纸带上选择0、1、2、3、4、5共6个计数点,相邻两计数点之间还有四个点未画出,纸带旁并排放着带有最小分度为毫米的刻度尺,零刻度线跟“0”计数点对齐,由图可以读出三个计数点1、3、5跟0点的距离填入下列表格中。

距离 | d1 | d2 | d3 |
测量值/cm |
①计算小车通过计数点“2”的瞬时速度公式为v2= (以d1、d2及相邻计数点间时间T来表示)代入得v2= m/s.(结果保留两位有效数字)
②加速度a=______(结果保留两位有效数字)