题目内容
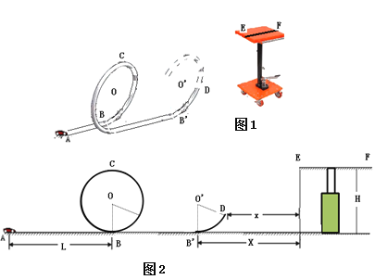
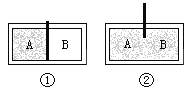
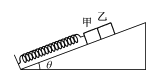
【题目】固定在水平地面的斜劈,其底端有一固定的挡板,质量为m的物块甲通过轻弹簧与挡板连接,另一完全相同的物块乙紧靠着物块甲,已知斜劈的倾角为θ,两物块与斜劈之间的动摩擦因数均为μ,开始时在物块乙上施加一沿斜劈向下的外力,使弹簧处于压缩状态,某时刻撤走外力, 当两物块沿斜劈向上运动的位移为x时,两物块具有最大速度v,最终两物块分离。已知重力加速度为g,则下列正确的说法是( )
A.两物块沿斜劈向上运动的位移为x时,轻弹簧的形变量为零
B.两物块刚好分离时,物块甲的加速度大小为![]()
C.从撤走外力到两物块具有最大速度,轻弹簧对物块甲做的功为![]()
D.从撤走外力到两物块具有最大速度,物块甲对物块乙做的功为![]()
【答案】BD
【解析】
A.两物块沿斜劈向上运动的位移为x时,两物块具有最大速度v,两物块的加速度为零,弹簧弹力
![]()
此时弹簧处于压缩状态,弹簧的形变量不为零,故A项错误;
B.两物块刚好分离时,两物块之间的相互作用力为零,两物块的加速度相同,则对乙受力分析,可得
![]()
故B项正确;
CD.从撤走外力到两物块具有最大速度,对甲、乙两物块组成的整体由动能定理得
![]()
解得:轻弹簧对物块甲做的功
![]()
从撤走外力到两物块具有最大速度,对乙物块由动能定理得
![]()
解得:物块甲对物块乙做的功
![]()
故C项错误,D项正确。

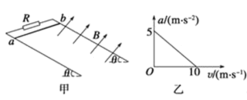
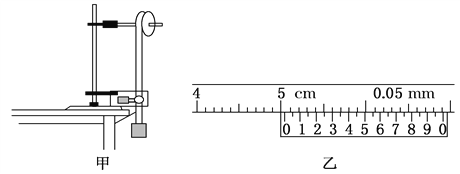
【题目】如图甲为研究“转动动能与角速度关系”的实验装置示意图,现有的器材为:固定在竖直平面内的转盘(转轴水平)、带铁夹的铁架台、电磁打点计时器(接交流电的频率为50 Hz)、纸带、重锤、游标卡尺、天平.回答下列问题 :
(1)如图乙所示,用20分度的游标卡尺测得圆盘的直径d为________ cm;
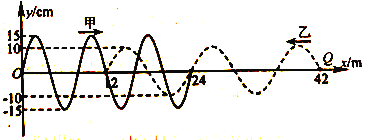
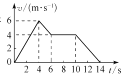
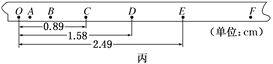
(2)将悬挂铁锤的纸带穿过打点计时器后,绕在转盘边缘上,纸带一端固定在转盘上,使得转盘与纸带不打滑,设纸带厚度不计,接通电源,释放重锤,打点计时器打出的纸带如图丙所示,O、A、B、C…各点为连续打出的点迹,则由图丙中数据可得,打下点迹D时,圆盘转动的角速度为ωD=____________ rad/s(保留三位有效数字);
(3)下表为各点对应的转动动能Ek和角速度ω值,请你猜想转动动能Ek和角速度ω满足的关系式为Ek=____________(须填写定量表达式).
计数点 | A | B | C | … | E |
转动动能Ek(J) | 0.001 0 | 0.003 9 | 0.008 9 | … | 0.024 |
角速度ω(rad/s) | 4.0 | 7.9 | 11.9 | … | 19.7 |