题目内容
【题目】如图所示,带等量异种电荷的A、B两板水平放置,在A、B间形成竖直向下的匀强电场。a、b两质量相等的粒子从A板左侧边缘处以相同的速度先后飞入电场,粒子a从A、B两板右端连线的中点飞离匀强电场,粒子b从B板右侧边缘处飞离匀强电场,不计粒子重力,下列说法中正确的是( )

A.粒子a、b的带电量之比为1∶2
B.电场对a、b粒子做功之比为1∶2
C.粒子a、b离开电场时的速度大小之比为1∶2
D.粒子a、b离开电场时的速度与水平方向之间夹角之比为1∶2
【答案】A
【解析】
A.设板长为L,带电粒子在电场中做类平抛运动,则竖直方向偏转位移为
![]()
由于粒子的质量相等、速度相等,偏转位移之比为1:2,则粒子a、b的带电量之比为1:2,故A正确;
B.根据电场力做功的计算公式可得
W=qEy
则电场对a、b粒子做功之比为1:4,故B错误;
C.根据动能定理可得
![]()
解得粒子离开电场的速度大小为
![]()
粒子a、b离开电场时的速度大小之比不等于1:2,故C错误;
D.设两板间的距离为d,粒子a、b离开电场时的速度与水平方向之间夹角分别为θa,θb,根据类平抛运动中速度方向反向延长线过水平位移的中点可得
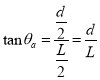

粒子a、b离开电场时的速度与水平方向之间夹角正切值之比为1:2,但是角度之比不等于1:2,故D错误。
故选A。

练习册系列答案
相关题目