题目内容
如图所示，一轻绳绕过两轻质滑轮，两端分别连接着矩形导线框A1和石块A2，线框A1的ab边长l1＝1 m，bc边长l2＝0.6 m，电阻R＝0.1 Ω，质量m＝0.5 kg，石块A2的质量M＝2 kg，两水平平行虚线ef、gh之间存在着垂直纸面向外的匀强磁场，磁感应强度B＝0.5 T，如果线框从静止开始运动，进入磁场最初一段时间是匀速的，ef和gh的距离s>l2（取g＝10 m/s2）。问：
（1）线框进入磁场前石块A2的加速度a为多大？
（2）线框进入磁场时匀速运动的速度v为多大？
（3）线框完全进入磁场后，ab边继续运动到gh线的过程中，其运动性质如何？
（1）线框进入磁场前石块A2的加速度a为多大？
（2）线框进入磁场时匀速运动的速度v为多大？
（3）线框完全进入磁场后，ab边继续运动到gh线的过程中，其运动性质如何？
解：（1）线框进入磁场前，线框A1仅受到细线的拉力FT和重力mg，石块A2受到重力Mg和拉力FT。由牛顿第二定律
对线框：FT－mg＝ma
对石块：Mg－FT＝Ma
联立解得：a＝
＝6 m/s2
（2）因为线框进入磁场的最初一段时间做匀速运动，所以石块受力平衡Mg＝FT′
线框abcd受力平衡FT′＝mg＋FA
ab边进入磁场切割磁感线，产生的电动势E＝Bl1v
形成的感应电流I＝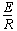
受到的安培力FA＝BIl1
联立上述各式得：Mg＝mg＋
代入数据解得v＝6 m/s
（3）线框完全进入磁场后到ab边运动至gh线，线框中无感应电流，受力情况同进入磁场前，所以该阶段仍做匀加速直线运动，加速度仍为a＝6 m/s2
对线框：FT－mg＝ma
对石块：Mg－FT＝Ma
联立解得：a＝
＝6 m/s2（2）因为线框进入磁场的最初一段时间做匀速运动，所以石块受力平衡Mg＝FT′
线框abcd受力平衡FT′＝mg＋FA
ab边进入磁场切割磁感线，产生的电动势E＝Bl1v
形成的感应电流I＝
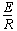
受到的安培力FA＝BIl1
联立上述各式得：Mg＝mg＋
代入数据解得v＝6 m/s
（3）线框完全进入磁场后到ab边运动至gh线，线框中无感应电流，受力情况同进入磁场前，所以该阶段仍做匀加速直线运动，加速度仍为a＝6 m/s2
练习册系列答案
名校课堂系列答案
相关题目
（2009?上海模拟）如图所示，一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量mB=m的小球连接，另一端与套在光滑直杆上质量mA=m的小物块连接，已知直杆两端固定，与两定滑轮在同一竖直平面内，与水平面的夹角θ=60°，直杆上C点与两定滑轮均在同一高度，C点到定滑轮O1的距离为L，重力加速度为g，设直杆足够长，小球运动过程中不会与其他物体相碰．现将小物块从C点由静止释放，试求：
如图所示，一轻绳绕过两轻质滑轮，两端分别连接着矩形导线框A和石块C，线框A的两边长分别为d=1m、l=0.6m，电阻R=0.1Ω，质量m=0.5kg，石块C质量M=2kg．线框正上方有垂直纸面向外的有界水平匀强磁场，磁感应强度B=0.5T，磁场宽度为s=1.6m．如果线框从图示位置由静止开始释放，则恰好能匀速进入磁场．取g=10m/s2．试求：
如图所示，一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量
如图所示，一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量为mB的小球连接，另一端与套在光滑直杆上质量mA的小物块连接，已知mA=mB=m，直杆两端固定，与两定滑轮在同一竖直平面内，与水平面的夹角θ=60°，直杆上C点与两定滑轮均在同一高度，C点到定滑轮O1的距离为L，重力加速度为g，设直杆足够长，小球运动过程中不会与其他物体相碰．现将小物块从C点由静止释放，试求：
（2009?枣庄一模）如图所示，一轻绳绕过无摩擦的两轻质的小定滑轮O1、O2跟质量为m的小球B连接，另一端与套在光滑直杆上质量也为m的小物块A连接．已知直杆两端固定，与两定滑轮在同一竖直平面内，与水平面的夹角θ=60°．直杆上C点与两定滑轮均在同一高度，C点到定滑轮O1的距离为L．设直杆足够长，小球运动过程中不会与其它物体相碰，重力加速度为g．现将小物块A从C点由静止释放．