题目内容
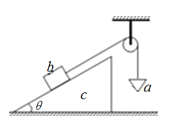
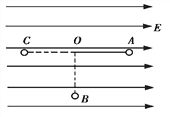
【题目】如图所示，固定的光滑斜面顶端有一定滑轮，绕过定滑轮的轻绳一端与斜面底端的木块相连，另一端绕过定滑轮与一小铁球相连，小球球心与斜面顶端等高；若由静止释放木块，小球落地后不再反弹，木块恰好能运动到斜面顶端；不计一切摩擦，运动过程中，木块和小球都可看做质点，已知斜面的倾角为θ=370，斜面顶端到地面的高度H=0.5m，重力加速度g=10m/s2，sin370=0.6，cos370=0.8，则木块上滑过程中，下列说法正确的是
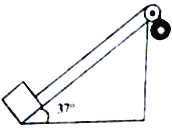
A. 小球的落地速度是2m/s
B. 小球经0.5s落地
C. 木块与小球的质量之比是5:3
D. 木块加速阶段的平均速度大于减速阶段的平均速度
【答案】AB
【解析】根据题意可知斜面长度
，故木块在斜面上运动时上滑0.5m过程中做加速运动，加速到v，平均速度为
，剩下
做减速运动，从v又减速到零，平均速度为
，两个过程中的平均速度相同，D错误；设滑块的质量为M，小球的质量为m，上滑加速位移
，上滑减速位移
，根据
可得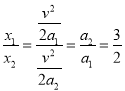
①，在上滑减速过程中，根据牛顿第二定律可得
，解得
，代入①可得
，根据
可得上滑加速时间，即小球下落时间
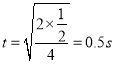，小球落地速度
，AB正确；根据牛顿第二定律，对小球可得
②，对滑块可得
③，联立②③可得
，C错误。
练习册系列答案
相关题目
