题目内容
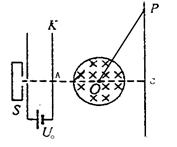
如图所示,S为离子源,从其小孔发射出电量为q的正离子(初速度可认为为零),经电压为U0的电场加速后,沿AC方向进入匀强磁场中。磁场被限制在以O为圆心r为半径的圆形区域内,磁感应强度大小为B,方向垂直纸面向里。正离子从磁场射出后,打在屏上的P点,偏转距离CP与屏到O点的距离OC之比CP:OC= 。求:(1)正离子的质量;
。求:(1)正离子的质量;

(2)正离子通过磁场所需的时间。
 。求:(1)正离子的质量;
。求:(1)正离子的质量;
(2)正离子通过磁场所需的时间。
(1) 3qB2r2/2U0 (2)πBr2/2U
(1)带电粒子从静止开始先在加速电场中做匀加速直线运动,
由动能定理得:
qUo=mv2/2-0 ①
在磁场中匀速圆周运动的运动轨迹如
图所示,粒子才能出磁
场后匀速直线运动打在屏上的P点,
在磁场中解三角形得半径
R= r ②
r ②
qvB=mv2/R ③
联立以上三式得m=3qB2r2/2U0
(2)由图可知,
∵CP:OC= ∴∠POC=60° ∴∠AOP=120°∴∠α=60°
∴∠POC=60° ∴∠AOP=120°∴∠α=60°
所以带电粒子在磁场中运动的时间为其周期的1/6
∵T=2πm/qB
∴t=T/6=πm/3qB=πBr2/2U。

由动能定理得:
qUo=mv2/2-0 ①
在磁场中匀速圆周运动的运动轨迹如
图所示,粒子才能出磁
场后匀速直线运动打在屏上的P点,
在磁场中解三角形得半径
R=
 r ②
r ② qvB=mv2/R ③
联立以上三式得m=3qB2r2/2U0
(2)由图可知,
∵CP:OC=
 ∴∠POC=60° ∴∠AOP=120°∴∠α=60°
∴∠POC=60° ∴∠AOP=120°∴∠α=60°所以带电粒子在磁场中运动的时间为其周期的1/6
∵T=2πm/qB
∴t=T/6=πm/3qB=πBr2/2U。

练习册系列答案
相关题目





 kg、电量q=2.5×
kg、电量q=2.5×
 m/s的速度射入磁场,带电粒子质量m=2.0×
m/s的速度射入磁场,带电粒子质量m=2.0× kg,所带电量q=-8.0×
kg,所带电量q=-8.0× C,粒子恰从c处射出磁场,求该磁场的磁感强度.若在该区域再平行于ab加一向左的匀强电场,电场强度E=5.0×
C,粒子恰从c处射出磁场,求该磁场的磁感强度.若在该区域再平行于ab加一向左的匀强电场,电场强度E=5.0× V/m,上述从e处射入的粒子当离开该区域时,速度有多大?(粒子重力忽略不计)
V/m,上述从e处射入的粒子当离开该区域时,速度有多大?(粒子重力忽略不计)
 的微粒沿半径为
的微粒沿半径为 的竖直圆周匀速运动,当与原静止在圆周上的另一带有电量-
的竖直圆周匀速运动,当与原静止在圆周上的另一带有电量- 的微粒相碰后,合在一起沿半径为
的微粒相碰后,合在一起沿半径为 的圆周匀速运动,则
的圆周匀速运动,则